Multiple Choice
Based on the graph , describe all points where the derivative would have a jump.
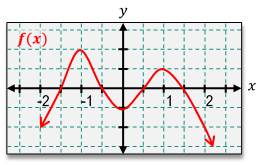
(-∞,-1) U (0,1)
(-1,0) U (1,∞)
(-∞, -1) U (1,∞)
(-1,1)
 Verified step by step guidance
Verified step by step guidance
 6:15m
6:15mMaster Graphing The Derivative with a bite sized video explanation from Patrick
Start learning
