Concavity: Videos & Practice Problems

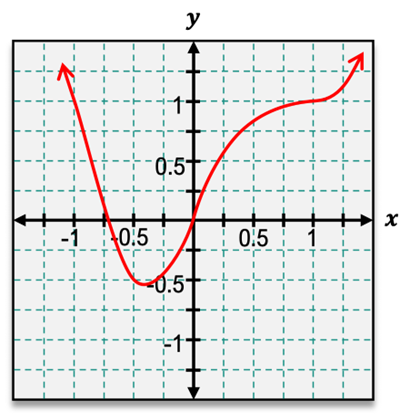
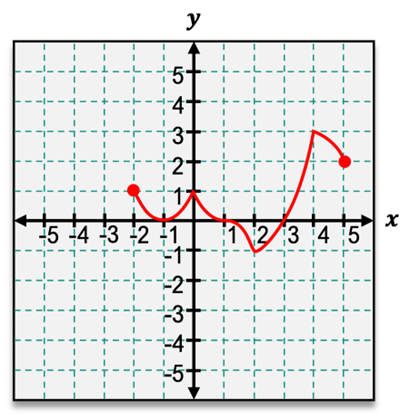
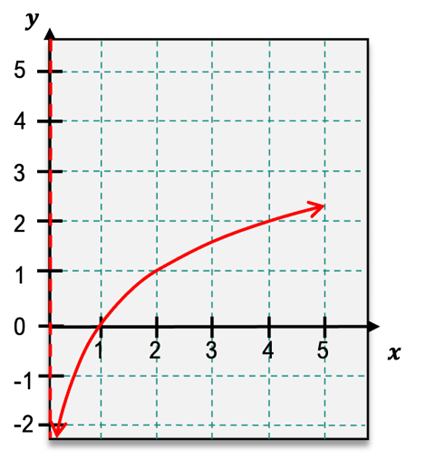
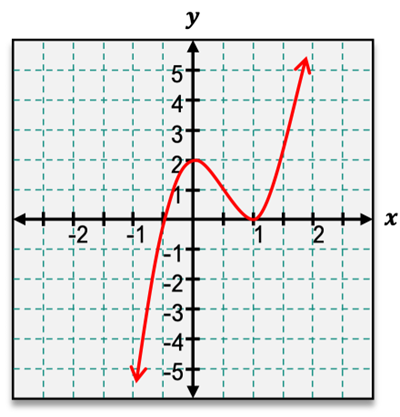
Understanding the concavity of a function is essential in analyzing its behavior. The concavity is determined by the sign of the second derivative of the function. When the second derivative is positive, the function is said to be concave up, resembling a smiley face on a graph. Conversely, when the second derivative is negative, the function is concave down, resembling a frowning face. This visual representation aids in recognizing the concavity of a function.

The first derivative of a function indicates its slope or rate of change. The second derivative, therefore, represents the rate of change of the first derivative, which can be interpreted as how the slope itself is changing. For instance, if the slope is increasing, the second derivative is positive, indicating concavity upwards. If the slope is decreasing, the second derivative is negative, indicating concavity downwards.

When analyzing a graph, tangent lines can be drawn to observe the behavior of the slope. In regions where the function is concave up, the tangent lines will lie below the curve, while in regions where the function is concave down, the tangent lines will lie above the curve. This relationship provides a helpful visual cue for identifying concavity.

A critical concept related to concavity is the inflection point, which occurs where the function changes concavity. At an inflection point, the second derivative is either zero or does not exist. This is similar to critical points for the first derivative, where the slope changes from increasing to decreasing or vice versa.

To determine intervals of concavity and identify inflection points, one can analyze the graph from left to right. For example, if a function starts off concave down and transitions to concave up, the point where this change occurs is an inflection point. By drawing tangent lines and observing their positions relative to the curve, one can effectively identify these intervals and points of inflection.

In summary, the concavity of a function, indicated by the sign of its second derivative, provides valuable insights into the function's behavior. Recognizing concave up and concave down regions, along with identifying inflection points, enhances the understanding of how a function behaves across its domain.

Understanding the concavity of a function is essential in calculus, as it provides insights into the behavior of the function's graph. Concavity refers to the direction in which a function curves. A function is said to be concave up when its graph opens upwards, resembling a cup, and concave down when it opens downwards, resembling an upside-down cup. The point at which a function changes from concave up to concave down (or vice versa) is known as an inflection point.

The concavity of a function can be determined by examining its second derivative. If the second derivative, denoted as f''(x), is positive (f''(x) > 0), the function is concave up. Conversely, if the second derivative is negative (f''(x) < 0), the function is concave down. This relationship allows us to analyze the concavity of a function even when we are given the graph of its second derivative. When the graph of the second derivative is above the x-axis, it indicates that the second derivative is positive, and thus the original function is concave up. When the graph is below the x-axis, the second derivative is negative, indicating that the original function is concave down.

To locate the inflection point using the graph of the second derivative, look for the x-value where the graph crosses the x-axis, as this signifies a change in the sign of the second derivative.

In addition to the second derivative, the first derivative of a function, denoted as f'(x), can also provide information about concavity. The second derivative represents the rate of change of the first derivative. If the first derivative is increasing, the original function is concave up; if the first derivative is decreasing, the original function is concave down. Thus, by analyzing the graph of the first derivative, one can determine the concavity of the original function in a similar manner.

In summary, when assessing the concavity of a function, it is crucial to identify which graph is presented: the graph of the function itself, its first derivative, or its second derivative. By understanding the relationships between these derivatives and their respective graphs, one can effectively determine the concavity and locate inflection points of the original function.

Understanding the behavior of a function involves analyzing its increasing and decreasing intervals, concavity, and points of inflection. A function is considered increasing when it moves upward as you move from left to right, while it is decreasing when it moves downward. To identify these intervals, we can examine the graph of the function.

For instance, if we start at an endpoint, say at \( x = -5 \), and observe that the function decreases until \( x = -4 \), we can conclude that the function is decreasing in the interval \((-5, -4)\). It then increases from \( x = -4 \) to \( x = -2\), indicating an increasing interval of \((-4, -2)\). Continuing this process, we can identify all intervals of increasing and decreasing behavior throughout the function.

Next, we analyze the concavity of the function. A function is concave up if it resembles a smile (the curve opens upwards) and concave down if it resembles a frown (the curve opens downwards). This can be determined by examining the position of tangent lines relative to the curve. If the tangent line lies below the curve, the function is concave up; if it lies above, the function is concave down.

For example, if we find that the function is concave up from \( x = -5 \) to \( x = -3 \) and then transitions to concave down until \( x = 0\), we can mark these intervals accordingly. The points where the concavity changes are known as points of inflection. These points can be identified at the boundaries of the concavity intervals.

To summarize the points of inflection, we note the coordinates where the concavity changes. For instance, if the function changes from concave up to concave down at \( x = -3 \) with a corresponding \( y \)-value of 1, the point of inflection is \((-3, 1)\). Similarly, we can identify other points of inflection at \( (0, -2) \), \( (2, -3) \), and \( (4, -3) \).

It is crucial to differentiate between increasing/decreasing behavior and concavity. The first derivative of a function indicates whether it is increasing or decreasing, while the second derivative indicates concavity. A function can be increasing while being concave down, and vice versa. Understanding these distinctions is essential for a comprehensive analysis of the function's behavior.

Understanding concavity is essential in calculus, as it provides insights into the behavior of functions. The concavity of a function is determined by the sign of its second derivative. If the second derivative is positive, the function is concave up, resembling a "smile," while a negative second derivative indicates the function is concave down, resembling a "frown." An important aspect to note is that concavity can change at points known as inflection points, where the second derivative is either zero or does not exist.

To analyze concavity without a graph, one must identify potential inflection points by finding where the second derivative equals zero or is undefined. The process begins with calculating the first derivative of the function, followed by the second derivative. For example, consider the function \( f(x) = 2x^3 + 12x^2 + 9x - 4 \). The first derivative, calculated using the power rule, is \( f'(x) = 6x^2 + 24x \). Differentiating again yields the second derivative \( f''(x) = 12x + 24 \), which can be factored to \( f''(x) = 12(x + 2) \).

Setting the second derivative equal to zero helps identify potential inflection points. In this case, solving \( 12(x + 2) = 0 \) gives \( x = -2 \). This point is a candidate for an inflection point, but further analysis is required to confirm a change in concavity.

Next, a sign chart is created based on the potential inflection point, dividing the number line into intervals: \( (-\infty, -2) \) and \( (-2, \infty) \). To determine the sign of the second derivative in these intervals, test values are chosen. For the interval \( (-\infty, -2) \), selecting \( x = -3 \) results in \( f''(-3) = 12(-3 + 2) = 12(-1) = -12 \), indicating that the function is concave down in this interval.

For the interval \( (-2, \infty) \), using \( x = 0 \) gives \( f''(0) = 12(0 + 2) = 24 \), which is positive, indicating that the function is concave up in this interval. Thus, the function is concave down from \( (-\infty, -2) \) and concave up from \( (-2, \infty) \).

Since the concavity changes at \( x = -2 \), this point is confirmed as an inflection point. Understanding these concepts allows for a deeper analysis of functions, enhancing the ability to predict their behavior without relying solely on graphical representations.

To determine the concavity of the function \( f(x) = 9x^{\frac{1}{5}} \), we need to analyze its second derivative. The concavity of a function is indicated by the sign of the second derivative: if it is positive, the function is concave up; if negative, it is concave down. Inflection points occur where the concavity changes, which is identified by finding where the second derivative is equal to zero or does not exist.

First, we find the first derivative using the power rule:

\( f'(x) = \frac{9}{5} x^{-\frac{4}{5}} \)

Next, we differentiate again to find the second derivative:

\( f''(x) = -\frac{36}{25} x^{-\frac{9}{5}} \)

To analyze potential inflection points, we set the second derivative equal to zero or find where it does not exist. Since the numerator is a constant and does not equal zero, we focus on where the second derivative does not exist, which occurs when the denominator is zero. This happens at:

\( x = 0 \)

Now, we create a sign chart to evaluate the intervals of concavity. The critical point \( x = 0 \) divides the number line into two intervals: \( (-\infty, 0) \) and \( (0, \infty) \). We will test a point from each interval in the second derivative.

For the interval \( (-\infty, 0) \), we can choose \( x = -1 \):

\( f''(-1) = -\frac{36}{25} (-1)^{-\frac{9}{5}} \)

Since \( (-1)^{-\frac{9}{5}} \) is negative, \( f''(-1) \) is positive, indicating that the function is concave up on \( (-\infty, 0) \).

For the interval \( (0, \infty) \), we can choose \( x = 1 \):

\( f''(1) = -\frac{36}{25} (1)^{-\frac{9}{5}} \)

This results in a negative value, indicating that the function is concave down on \( (0, \infty) \).

From this analysis, we conclude that the function is concave up on the interval \( (-\infty, 0) \) and concave down on the interval \( (0, \infty) \). The point \( x = 0 \) is an inflection point since the concavity changes at this point.

To find the coordinates of the inflection point, we evaluate the original function at \( x = 0 \):

\( f(0) = 9 \cdot 0^{\frac{1}{5}} = 0 \)

Thus, the inflection point is located at the ordered pair \( (0, 0) \).

To analyze the concavity of the polynomial function f(x) = 5x² - 2x + 24, we begin by determining its first and second derivatives. The first derivative, calculated using the power rule, is:

f'(x) = 10x - 2

Next, we find the second derivative by differentiating the first derivative:

f''(x) = 10

To identify potential inflection points, we look for values where the second derivative is equal to zero or does not exist. In this case, since f''(x) = 10 is a constant positive value, it is never equal to zero and does not have any points of discontinuity. Therefore, there are no potential inflection points.

Since the second derivative is positive everywhere, we conclude that the function is concave up across its entire domain. Specifically, the function is concave up on the interval:

(−∞, +∞)

Given that the concavity does not change, the function has no inflection points. This behavior aligns with the characteristics of a quadratic function that opens upwards, as indicated by the positive coefficient of the x² term.