Corporate Officers and Committees The Self Driving Unicycle Company was recently successfully funded via Kickstarter and must now appoint a president, chief executive officer (CEO), chief operating officer (COO), and chief financial officer (CFO), and chief human resources officer (CHR). It must also appoint a strategic planning committee with five different members. There are 15 qualified candidates, and officers can also serve on the committee.

b. How many different ways can a committee of five be appointed?

Denomination Effect

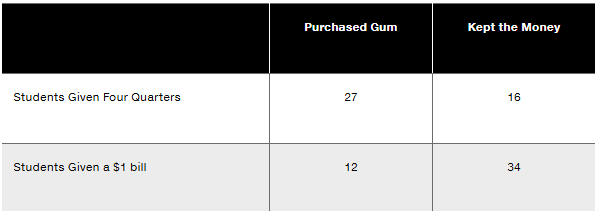
In Exercises 13–16, use the data in the following table. In an experiment to study the effects of using four quarters versus a $1 bill, some college students were given four quarters and others were given a $1 bill, and they could either keep the money or spend it on gum. The results are summarized in the table (based on data from “The Denomination Effect,” by Priya Raghubir and Joydeep Srivastava, Journal of Consumer Research, Vol. 36).

Denomination Effect

b. Find the probability of randomly selecting a student who kept the money, given that the student was given four quarters.

Dice and Coins

c. Find the probability that when a six-sided die is rolled, the outcome is 7.

Kentucky Derby Odds When the horse Justify won the 144th Kentucky Derby, a $2 bet on a Justify win resulted in a winning ticket worth $7.80.

c. If the payoff odds were the actual odds found in part (c), what would be the worth of a $2 win ticket after the Justify win?

ATM You want to obtain cash by using an ATM, but it’s dark and you can’t see your card when you insert it. The card must be inserted with the front side up and the printing configured so that the beginning of your name enters first.

c. How many random selections are required to be absolutely sure that the card works because it is inserted correctly?

In Exercises 21–24, use these results from the “1-Panel-THC” test for marijuana use, which is provided by the company Drug Test Success: Among 143 subjects with positive test results, there are 24 false positive (incorrect) results; among 157 negative results, there are 3 false negative (incorrect) results. (Hint: Construct a table similar to Table 4-1.)

Testing for Marijuana Use

c. What is the probability that a randomly selected subject had a true negative result?

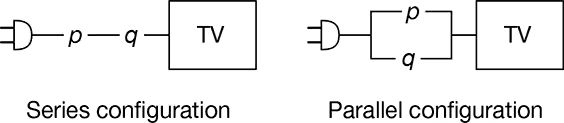
Surge Protectors Refer to the accompanying figure showing surge protectors p and q used to protect an expensive television. If there is a surge in the voltage, the surge protector reduces it to a safe level. Assume that each surge protector has a 0.985 probability of working correctly when a voltage surge occurs.

c. Which arrangement should be used for better protection?

Organ Donors USA Today provided information about a survey (conducted for Donate Life America) of 5100 adult Internet users. Of the respondents, 2346 said they are willing to donate organs after death. In this survey, 100 adults were surveyed in each state and the District of Columbia, and results were weighted to account for the different state population sizes.

b. Based on the poll results, what is the probability of randomly selecting an adult who is willing to donate organs after death?

In Exercises 21-28, find the probability and answer the questions.

X-Linked Genetic Disease Men have XY (or YX) chromosomes and women have XX chromosomes. X-linked recessive genetic diseases (such as juvenile retinoschisis) occur when there is a defective X chromosome that occurs without a paired X chromosome that is not defective. In the following, represent a defective X chromosome with lowercase x, so a child with the xY or Yx pair of chromosomes will have the disease and a child with XX or XY or YX or xX or Xx will not have the disease. Each parent contributes one of the chromosomes to the child.

c. If a mother has one defective x chromosome and one good X chromosome and the father has good XY chromosomes, what is the probability that a son will inherit the disease?

Phase I of a Clinical Trial A clinical test on humans of a new drug is normally done in three phases. Phase I is conducted with a relatively small number of healthy volunteers. For example, a phase I test of bexarotene involved only 14 subjects. Assume that we want to treat 14 healthy humans with this new drug and we have 16 suitable volunteers available.

c. If 14 subjects are randomly selected and treated at the same time, what is the probability of selecting the 14 youngest subjects?

Florida Pick 3 In the Florida Pick 3 lottery, you can place a “straight” bet of $1 by selecting the exact order of three digits between 0 and 9 inclusive (with repetition allowed), so the probability of winning is 1/1000. If the same three numbers are drawn in the same order, you collect $500, so your net profit is $499.

c. Is there much of a difference between the actual odds against winning and the payoff odds?

Mega Millions As of this writing, the Mega Millions lottery is run in 44 states. Winning the jackpot requires that you select the correct five different numbers from 1 to 70 and, in a separate drawing, you must also select the correct single number from 1 to 25.

c. How does the probability compare to the probability for the old Mega Millions game which involved the selection of five different numbers between 1 and 75 and a separate single number between 1 and 15?

Sampling Eye Color Based on a study by Dr. P. Sorita Soni at Indiana University, assume that eye colors in the United States are distributed as follows: 40% brown, 35% blue, 12% green, 7% gray, 6% hazel.

d. If two people are randomly selected, what is the probability that at least one of them has brown eyes?

Births in the United States In the United States, the true probability of a baby being a boy is 0.512 (based on the data available at this writing). For a family having three children, find the following.

d. The probability that at least one of the children is a girl.

Subjective Probability Estimate the probability that the next time you watch a TV news report, it includes a story about a plane crash.

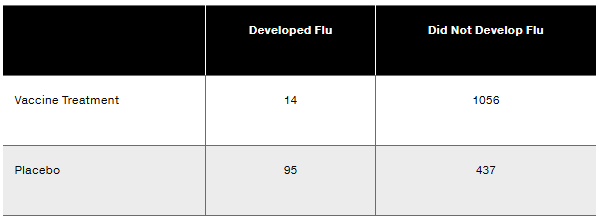
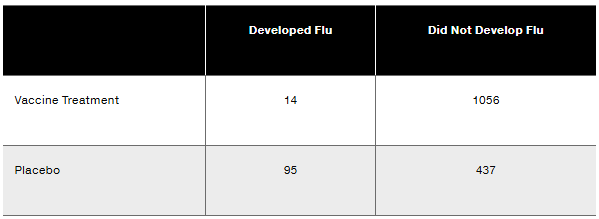
In Exercises 6–10, use the following results from tests of an experiment to test the effectiveness of an experimental vaccine for children (based on data from USA Today). Express all probabilities in decimal form.

If 1 of the 1602 subjects is randomly selected, find the probability of getting 1 who had the vaccine treatment and developed flu.

Standard Tests Standard tests, such as the SAT or ACT or MCAT, tend to make extensive use of multiple-choice questions because they are easy to grade using software. If one such multiple choice question has possible correct answers of a, b, c, d, e, what is the probability of a wrong answer if the answer is a random guess?

ESP A psychologist tells you that in an ESP (extrasensory perception) experiment, there is a 20% chance of answering a question correctly. What is the probability of answering a question correctly?

In Exercises 6–10, use the following results from tests of an experiment to test the effectiveness of an experimental vaccine for children (based on data from USA Today). Express all probabilities in decimal form.

If 1 of the 1602 subjects is randomly selected, find the probability of getting 1 that developed flu.

National Statistics Day

b. If a person is randomly selected, find the probability that his or her birthday is in October. Ignore leap years.

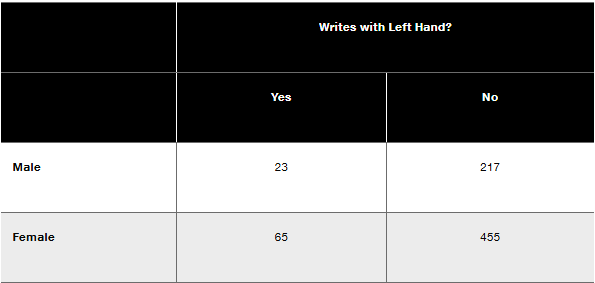
In Exercises 1–10, use the data in the accompanying table and express all results in decimal form. (The data are from “The Left-Handed: Their Sinister History,” by Elaine Fowler Costas, Education Resources Information Center, Paper 399519.)

Complement If L represents the event of randomly selecting one of the study subjects and getting someone who writes with their left hand, what does L represent? Find the value of P(L)

Vision Correction About 75% of the U.S. population uses some type of vision correction (such as glasses or contact lenses).

d. If you randomly select four people, is a result of all four using vision correction significantly high? Why or why not?