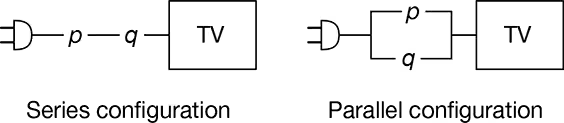
Surge Protectors Refer to the accompanying figure showing surge protectors p and q used to protect an expensive television. If there is a surge in the voltage, the surge protector reduces it to a safe level. Assume that each surge protector has a 0.985 probability of working correctly when a voltage surge occurs.

c. Which arrangement should be used for better protection?

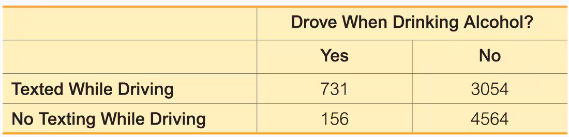
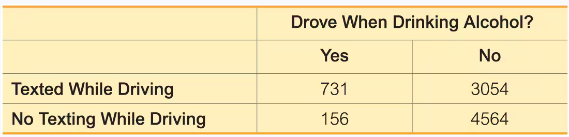
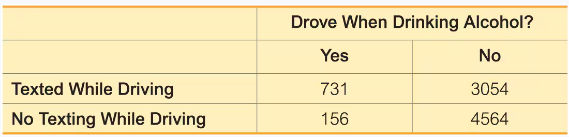
In Exercises 9–20, use the data in the following table, which lists survey results from high school drivers at least 16 years of age (based on data from “Texting While Driving and Other Risky Motor Vehicle Behaviors Among U.S. High School Students,” by O’Malley, Shults, and Eaton, Pediatrics, Vol. 131, No. 6). Assume that subjects are randomly selected from those included in the table. Hint: Be very careful to read the question correctly.

Drinking and Driving If two of the high school drivers are randomly selected, find the probability that they both drove when drinking alcohol.

b. Assume that the selections are made without replacement. Are the events independent?

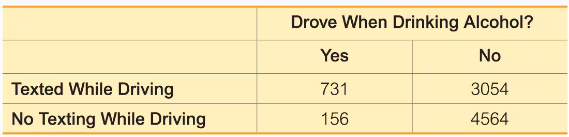
In Exercises 9–20, use the data in the following table, which lists survey results from high school drivers at least 16 years of age (based on data from “Texting While Driving and Other Risky Motor Vehicle Behaviors Among U.S. High School Students,” by O’Malley, Shults, and Eaton, Pediatrics, Vol. 131, No. 6). Assume that subjects are randomly selected from those included in the table. Hint: Be very careful to read the question correctly.

Texting While Driving If two of the high school drivers are randomly selected, find the probability that they both texted while driving.

a. Assume that the selections are made with replacement. Are the events independent?

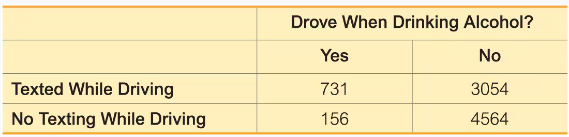
In Exercises 9–20, use the data in the following table, which lists survey results from high school drivers at least 16 years of age (based on data from “Texting While Driving and Other Risky Motor Vehicle Behaviors Among U.S. High School Students,” by O’Malley, Shults, and Eaton, Pediatrics, Vol. 131, No. 6). Assume that subjects are randomly selected from those included in the table. Hint: Be very careful to read the question correctly.

Texting and Alcohol If three of the high school drivers are randomly selected from the 4720 subjects who did not text while driving, find the probability that all three drove when drinking.

a. Assume that the selections are made with replacement. Are the events independent?

In Exercises 9–20, use the data in the following table, which lists survey results from high school drivers at least 16 years of age (based on data from “Texting While Driving and Other Risky Motor Vehicle Behaviors Among U.S. High School Students,” by O’Malley, Shults, and Eaton, Pediatrics, Vol. 131, No. 6). Assume that subjects are randomly selected from those included in the table. Hint: Be very careful to read the question correctly.

Texting and Alcohol If one of the high school drivers is randomly selected, find the probability that the selected driver did not text while driving and did not drive when drinking.

In Exercises 9–20, use the data in the following table, which lists survey results from high school drivers at least 16 years of age (based on data from “Texting While Driving and Other Risky Motor Vehicle Behaviors Among U.S. High School Students,” by O’Malley, Shults, and Eaton, Pediatrics, Vol. 131, No. 6). Assume that subjects are randomly selected from those included in the table. Hint: Be very careful to read the question correctly.

Texting and Alcohol If four different high school drivers are randomly selected, find the probability that they all texted while driving.

In Exercises 21–24, use these results from the “1-Panel-THC” test for marijuana use, which is provided by the company Drug Test Success: Among 143 subjects with positive test results, there are 24 false positive (incorrect) results; among 157 negative results, there are 3 false negative (incorrect) results. (Hint: Construct a table similar to Table 4-1.)

Testing for Marijuana Use

a. How many subjects are included in the study?

Redundancy in Computer Hard Drives It is generally recognized that it is wise to backup computer data. Assume that the following refer to use of Western Digital model WD60EFRX hard drives, which have an annual failure rate of 3.66% (based on data from Backblaze, Inc.).

a. If you store all of your computer data on a single hard drive, what is the probability that the drive will fail during a year?

Alarm Clock Life Hack Each of us must sometimes wake up early for something really important, such as a final exam, job interview, or an early flight. (Professional golfer Jim Furyk was disqualified from a tournament when his cellphone lost power and he overslept.) Assume that a battery-powered alarm clock has a 0.005 probability of failure, a smartphone alarm clock has a 0.052 probability of failure, and an electric alarm clock has a 0.001 probability of failure.

a. What is the probability that your single battery-powered alarm clock works successfully when you need it?

Births in Vietnam In Vietnam, the probability of a baby being a boy is 0.526 (based on the data available at this writing). For a family having four children, find the following.

b. The probability that all four children are girls.

Denomination Effect

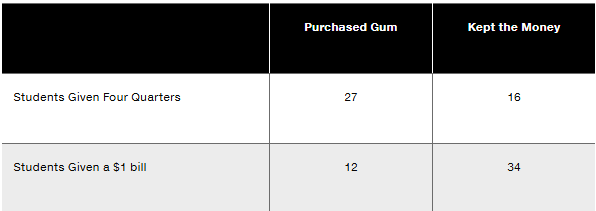
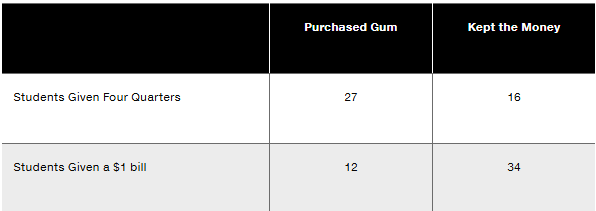
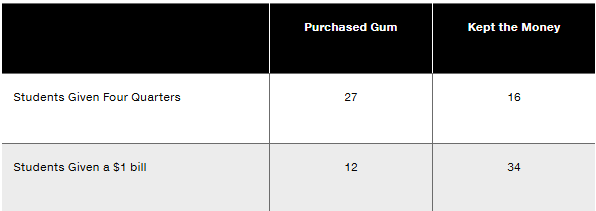
In Exercises 13–16, use the data in the following table. In an experiment to study the effects of using four quarters versus a $1 bill, some college students were given four quarters and others were given a $1 bill, and they could either keep the money or spend it on gum. The results are summarized in the table (based on data from “The Denomination Effect,” by Priya Raghubir and Joydeep Srivastava, Journal of Consumer Research, Vol. 36).

Denomination Effect

b. Find the probability of randomly selecting a student who kept the money, given that the student was given four quarters.

Denomination Effect

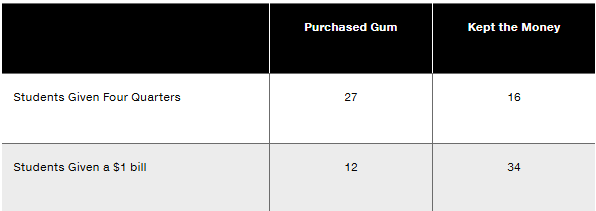
In Exercises 13–16, use the data in the following table. In an experiment to study the effects of using four quarters versus a $1 bill, some college students were given four quarters and others were given a $1 bill, and they could either keep the money or spend it on gum. The results are summarized in the table (based on data from “The Denomination Effect,” by Priya Raghubir and Joydeep Srivastava, Journal of Consumer Research, Vol. 36).

Denomination Effect

a. Find the probability of randomly selecting a student who spent the money, given that the student was given a $1 bill.

Denomination Effect

In Exercises 13–16, use the data in the following table. In an experiment to study the effects of using four quarters versus a $1 bill, some college students were given four quarters and others were given a $1 bill, and they could either keep the money or spend it on gum. The results are summarized in the table (based on data from “The Denomination Effect,” by Priya Raghubir and Joydeep Srivastava, Journal of Consumer Research, Vol. 36).

Denomination Effect

a. Find the probability of randomly selecting a student who spent the money, given that the student was given four quarters.

Denomination Effect

In Exercises 13–16, use the data in the following table. In an experiment to study the effects of using four quarters versus a $1 bill, some college students were given four quarters and others were given a $1 bill, and they could either keep the money or spend it on gum. The results are summarized in the table (based on data from “The Denomination Effect,” by Priya Raghubir and Joydeep Srivastava, Journal of Consumer Research, Vol. 36).

Denomination Effect

a. Find the probability of randomly selecting a student who kept the money, given that the student was given four quarters.

In Exercises 17–20, refer to the accompanying table showing results from experiments conducted by researchers Charles R. Honts (Boise State University) and Gordon H. Barland (Department of Defense Polygraph Institute). In each case, it was known whether or not the subject lied, so the table indicates when the polygraph (lie detector) test was correct.

False Negative Find the probability of selecting a subject with a negative polygraph result, given that the subject lied. What would be an unfavorable consequence of this error?

Language: Complement of “At Least One” Let A=the event of getting at least one defective calculator when four are randomly selected with replacement from a batch. Write a statement describing event A

Notation For a polygraph (lie detector) used when a subject is presented with a question, let L= the subject lied and let Y = the polygraph indicated that the subject told a lie. Use your own words to translate the notation P (Y|L) into a verbal statement.

Probability of a Girl Assuming that boys and girls are equally likely, find the probability of a couple having a boy when their third child is born, given that the first two children were both girls.

Births in the United States In the United States, the true probability of a baby being a boy is 0.512 (based on the data available at this writing). For a family having three children, find the following.

b. The probability that all three children are boys.

Births in the United States In the United States, the true probability of a baby being a boy is 0.512 (based on the data available at this writing). For a family having three children, find the following.

d. The probability that at least one of the children is a girl.

Redundancy in Computer Hard Drives The Seagate ST8000NM0055 hard drive has a 1.22% rate of failures in a year (based on data from Backblaze, Inc.). For the following, assume that all hard drives are that Seagate model.

a. If all of your computer data are stored on a hard disk drive with a copy stored on a second hard disk drive, what is the probability that during a year, you can avoid catastrophe with at least one working drive? Express the result with six decimal places.

Composite Drug Test Based on the data in Table 4-1, assume that the probability of a randomly selected person testing positive for drug use is 0.126. If drug screening samples are collected from 5 random subjects and combined, find the probability that the combined sample will reveal a positive result. Is that probability low enough so that further testing of the individual samples is rarely necessary?

Shared Birthdays Find the probability that of 25 randomly selected people, at least 2 share the same birthday.

Unseen Coins A statistics professor tosses two coins that cannot be seen by any students. One student asks this question: “Did one of the coins turn up heads?” Given that the professor’s response is “yes,” find the probability that both coins turned up heads.

High Fives

b. If n mathletes shake hands with each other exactly once, what is the total number of handshakes?

In Exercises 21–24, use these results from the “1-Panel-THC” test for marijuana use, which is provided by the company Drug Test Success: Among 143 subjects with positive test results, there are 24 false positive (incorrect) results; among 157 negative results, there are 3 false negative (incorrect) results. (Hint: Construct a table similar to Table 4-1.)

Testing for Marijuana Use

c. What is the probability that a randomly selected subject had a true negative result?

Combination Lock The typical combination lock uses three numbers, each between 0 and 49. Opening the lock requires entry of the three numbers in the correct order. Is the name “combination” lock appropriate? Why or why not?

Social Security Numbers A Social Security number consists of nine digits in a particular order, and repetition of digits is allowed. After seeing the last four digits printed on a receipt, if you randomly select the other digits, what is the probability of getting the correct Social Security number of the person who was given the receipt?

Quinela In a horse race, a quinela bet is won if you selected the two horses that finish first and second, and they can be selected in any order. The 144th running of the Kentucky Derby had a field of 20 horses. What is the probability of winning a quinela bet if you randomly select the horses?

Radio Station Call Letters Radio and Television station call letters must begin with either K (for stations west of the Mississippi River) or W (for stations east of the Mississippi River) and must include either two or three additional letters. How many different possibilities are there?