In Exercises 33–40, use the given probability value to determine whether the sample results are significant.

Voting Repeat Exercise 33 after replacing 40 Democrats being placed on the first line of voting ballots with 27 Democrats being placed on the first line. The probability of getting a result as high as 27 is 0.029792.

In Exercises 33–40, use the given probability value to determine whether the sample results are significant.

Selfie Deaths Based on Priceonomics data describing 49 deaths while taking selfies, it was found that 37 of those deaths were males. Assuming that males and females are equally likely to have selfie deaths, there is a 0.000235 probability of getting 37 or more males. Is the result of 37 males significantly low, significantly high, or neither? Does the result suggest that male selfie deaths are more likely than female selfie deaths?

Florida Pick 3 In the Florida Pick 3 lottery, you can place a “straight” bet of $1 by selecting the exact order of three digits between 0 and 9 inclusive (with repetition allowed), so the probability of winning is 1/1000. If the same three numbers are drawn in the same order, you collect $500, so your net profit is $499.

a. Find the actual odds against winning.

Florida Pick 3 In the Florida Pick 3 lottery, you can place a “straight” bet of $1 by selecting the exact order of three digits between 0 and 9 inclusive (with repetition allowed), so the probability of winning is 1/1000. If the same three numbers are drawn in the same order, you collect $500, so your net profit is $499.

c. Is there much of a difference between the actual odds against winning and the payoff odds?

Finding Odds in Roulette A roulette wheel has 38 slots. One slot is 0, another is 00, and the others are numbered 1 through 36, respectively. You place a bet that the outcome is an odd number.

a. What is your probability of winning?

California Lottery Let A denote the event of placing a $1 straight bet on the California Daily 4 lottery and winning. There are 10,000 different ways that you can select the four digits (with repetition allowed) in this lottery, and only one of those four-digit numbers will be the winner. What is the value of P(A)? What is the value of P(Abar)?

Dice and Coins

c. Find the probability that when a six-sided die is rolled, the outcome is 7.

Subjective Probability Estimate the probability that the next time that you approach an escalator, you find it to be in operation.

Penicillin “Who discovered penicillin: Marcel Bich, William Penn, Jonas Salk, Alexander Fleming, or Louis Pasteur?” If you make a random guess for the answer to that question, what is the probability that your answer is the correct answer of Alexander Fleming?

In Exercises 9–12, assume that 100 births are randomly selected. Use subjective judgment to describe the given number of girls as (a) significantly low, (b) significantly high, or (c) neither significantly low nor significantly high.

53 girls.

In Exercises 9–12, assume that 100 births are randomly selected. Use subjective judgment to describe the given number of girls as (a) significantly low, (b) significantly high, or (c) neither significantly low nor significantly high.

75 girls.

In Exercises 13–20, express the indicated degree of likelihood as a probability value between 0 and 1.

SAT Test When making a random guess for an answer to a multiple choice question on an SAT test, the possible answers are a, b, c, d, e, so there is 1 chance in 5 of being correct.

In Exercises 13–20, express the indicated degree of likelihood as a probability value between 0 and 1.

Movies Based on a study of the movies made in a recent year, 33 out of every 100 movies have a female lead or co-lead.

In Exercises 13–20, express the indicated degree of likelihood as a probability value between 0 and 1.

Randomness When using a computer to randomly generate the last digit of a phone number to be called for a survey, there is 1 chance in 10 that the last digit is zero

In Exercises 13–20, express the indicated degree of likelihood as a probability value between 0 and 1.

Square Peg Sydney Smith wrote in “On the Conduct of the Understanding” that it is impossible to fit a square peg in a round hole.

Kentucky Derby Odds When the horse Justify won the 144th Kentucky Derby, a $2 bet on a Justify win resulted in a winning ticket worth $7.80.

a. How much net profit was made from a $2 win bet on Justify?

Kentucky Derby Odds When the horse Justify won the 144th Kentucky Derby, a $2 bet on a Justify win resulted in a winning ticket worth $7.80.

c. If the payoff odds were the actual odds found in part (c), what would be the worth of a $2 win ticket after the Justify win?

In Exercises 21–24, use these results from the “1-Panel-THC” test for marijuana use, which is provided by the company Drug Test Success: Among 143 subjects with positive test results, there are 24 false positive (incorrect) results; among 157 negative results, there are 3 false negative (incorrect) results. (Hint: Construct a table similar to Table 4-1.)

Testing for Marijuana Use

b. How many of the subjects had a true negative result?

In Exercises 21–24, use these results from the “1-Panel-THC” test for marijuana use, which is provided by the company Drug Test Success: Among 143 subjects with positive test results, there are 24 false positive (incorrect) results; among 157 negative results, there are 3 false negative (incorrect) results. (Hint: Construct a table similar to Table 4-1.)

Testing for Marijuana Use If one of the test subjects is randomly selected, find the probability that the subject tested positive or did not use marijuana.

Same Birthdays If 25 people are randomly selected, find the probability that no 2 of them have the same birthday. Ignore leap years.

Exclusive Or The exclusive or means either one or the other event occurs, but not both.

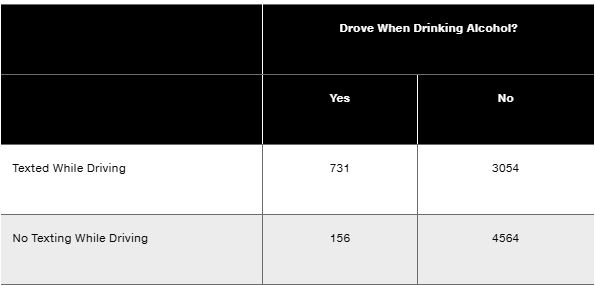
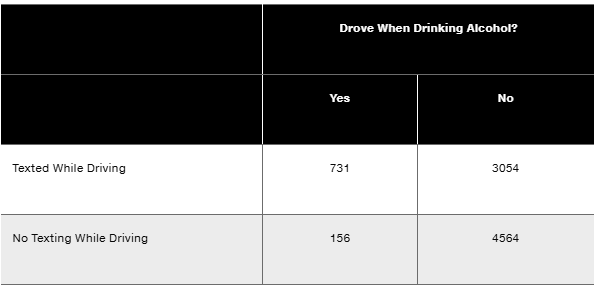
If one of the high school drivers is randomly selected, find the probability of getting one who texted while driving or drove when drinking alcohol.

b. Repeat Exercise 11 “Texting or Drinking” using the exclusive or instead of the inclusive or.

Notation When randomly selecting adults, let M denote the event of randomly selecting a male and let B denote the event of randomly selecting someone with blue eyes. What does P (M|B) represent? Is P (M|B) the same as P (B|M)?

Laundry Symbols Based on a New Generation of Stains survey, 13% of U.S. adults know that the care-instruction symbol on clothing means that any bleach can be used. Find the probability of randomly selecting an adult in the U.S. who does not know that.

In Exercises 9–20, use the data in the following table, which lists survey results from high school drivers at least 16 years of age (based on data from “Texting While Driving and Other Risky Motor Vehicle Behaviors Among U.S. High School Students,” by O’Malley, Shults, and Eaton, Pediatrics, Vol. 131, No. 6). Assume that subjects are randomly selected from those included in the table. Hint: Be very careful to read the question correctly.

Drinking and Driving If one of the high school drivers is randomly selected, find the probability of getting one who drove when drinking alcohol.

In Exercises 9–20, use the data in the following table, which lists survey results from high school drivers at least 16 years of age (based on data from “Texting While Driving and Other Risky Motor Vehicle Behaviors Among U.S. High School Students,” by O’Malley, Shults, and Eaton, Pediatrics, Vol. 131, No. 6). Assume that subjects are randomly selected from those included in the table. Hint: Be very careful to read the question correctly.

Texting or Drinking If one of the high school drivers is randomly selected, find the probability of getting one who texted while driving or drove when drinking alcohol.

Notation When randomly selecting a new smartphone, D denotes the event that it has a manufacturing defect. What do P(D) and P(D) represent?

Women in Movies In a recent year, speaking characters in movies were 68.2% male. What is the probability of randomly selecting a character with a speaking part and getting a female? What should be the value of that probability?

Alarm Clock Life Hack Each of us must sometimes wake up early for something really important, such as a final exam, job interview, or an early flight. (Professional golfer Jim Furyk was disqualified from a tournament when his cellphone lost power and he overslept.) Assume that a battery-powered alarm clock has a 0.005 probability of failure, a smartphone alarm clock has a 0.052 probability of failure, and an electric alarm clock has a 0.001 probability of failure.

b. If you use a battery-powered alarm clock and a smartphone alarm clock, what is the probability that they both fail? What is the probability that both of them do not fail?

In Exercises 29 and 30, find the probabilities and indicate when the “5% guideline for cumbersome calculations” is used.

Medical Helicopters In a study of helicopter usage and patient survival, results were obtained from 47,637 patients transported by helicopter and 111,874 patients transported by ground (based on data from “Association Between Helicopter vs Ground Emergency Medical Services and Survival for Adults with Major Trauma,” by Galvagno et al., Journal of the American Medical Association, Vol. 307, No. 15).

b. If 5 of the subjects in the study are randomly selected without replacement, what is the probability that all of them were transported by helicopter?

Surge Protectors Refer to the accompanying figure showing surge protectors p and q used to protect an expensive television. If there is a surge in the voltage, the surge protector reduces it to a safe level. Assume that each surge protector has a 0.985 probability of working correctly when a voltage surge occurs.

a. If the two surge protectors are arranged in series, what is the probability that a voltage surge will not damage the television? (Do not round the answer.)