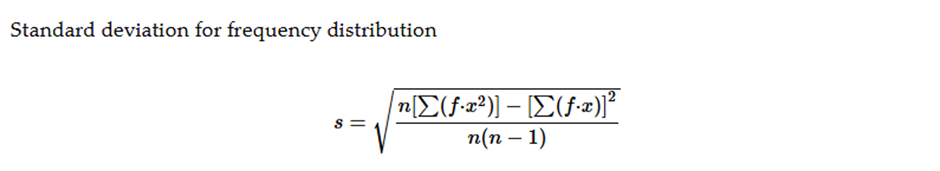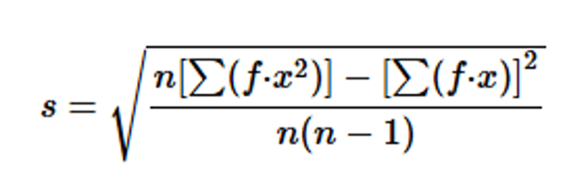Back
BackProblem 3.2.6
In Exercises 5–20, find the range, variance, and standard deviation for the given sample data. Include appropriate units (such as “minutes”) in your results. (The same data were used in Section 3-1, where we found measures of center. Here we find measures of variation.) Then answer the given questions.
Super Bowl Ages Listed below are the ages of the same 11 players used in the preceding exercise. How are the resulting statistics fundamentally different from those found in the preceding exercise?
41 24 30 31 32 29 25 26 26 25 30
Problem 3.2.35
Identifying Significant Values with the Range Rule of Thumb. In Exercises 33–36, use the range rule of thumb to identify the limits separating values that are significantly low or significantly high.
Foot Lengths Based on Data Set 9 “Foot and Height” in Appendix B, adult males have foot lengths with a mean of 27.32 cm and a standard deviation of 1.29 cm. Is the adult male foot length of 30 cm significantly low, significantly high, or neither? Explain.
Problem 3.2.33
Identifying Significant Values with the Range Rule of Thumb. In Exercises 33–36, use the range rule of thumb to identify the limits separating values that are significantly low or significantly high.
U.S. Presidents Based on Data Set 22 “Presidents” in Appendix B, at the time of their first inauguration, presidents have a mean age of 55.2 years and a standard deviation of 6.9 years. Is the minimum required 35-year age for a president significantly low?
Problem 3.2.31
Estimating Standard Deviation with the Range Rule of Thumb. In Exercises 29–32, refer to the data in the indicated exercise. After finding the range of the data, use the range rule of thumb to estimate the value of the standard deviation. Compare the result to the standard deviation computed using all of the data.
Audiometry Use the hearing measurements from Data Set 7 “Audiometry.” Does it appear that the amounts of variation are different for the right threshold measurements and the left threshold measurements?
Problem 3.2.9
In Exercises 5–20, find the range, variance, and standard deviation for the given sample data. Include appropriate units (such as “minutes”) in your results. (The same data were used in Section 3-1, where we found measures of center. Here we find measures of variation.) Then answer the given questions.
Jaws 3 Listed below are the number of unprovoked shark attacks worldwide for the last several years. What extremely important characteristic of the data is not considered when finding the measures of variation?
70 54 68 82 79 83 76 73 98 81
Problem 3.2.11
In Exercises 5–20, find the range, variance, and standard deviation for the given sample data. Include appropriate units (such as “minutes”) in your results. (The same data were used in Section 3-1, where we found measures of center. Here we find measures of variation.) Then answer the given questions.
Smart Thermostats Listed below are selling prices (dollars) of smart thermostats tested by Consumer Reports magazine. Are any of the resulting statistics helpful in selecting a smart thermostat for purchase?
250 170 225 100 250 250 130 200 150 250 170 200 180 250
Problem 3.2.19
In Exercises 5–20, find the range, variance, and standard deviation for the given sample data. Include appropriate units (such as “minutes”) in your results. (The same data were used in Section 3-1, where we found measures of center. Here we find measures of variation.) Then answer the given questions.
California Smokers In the California Health Interview Survey, randomly selected adults are interviewed. One of the questions asks how many cigarettes are smoked per day, and results are listed below for 50 randomly selected respondents. How well do the results reflect the smoking behavior of California adults?
[IMAGE]
Problem 3.2.26
Large Data Sets from Appendix B. In Exercises 25–28, refer to the indicated data set in Appendix B. Use software or a calculator to find the range, variance, and standard deviation. Express answers using appropriate units, such as “minutes.”
Earthquakes Use the magnitudes (Richter scale) of the 600 earthquakes listed in Data Set 24 “Earthquakes” in Appendix B. In 1989, the San Francisco Bay Area was struck with an earthquake that measured 7.0 on the Richter scale. If we add that value of 7.0 to those listed in the data set, do the measures of variation change much?
Problem 3.2.29
Estimating Standard Deviation with the Range Rule of Thumb. In Exercises 29–32, refer to the data in the indicated exercise. After finding the range of the data, use the range rule of thumb to estimate the value of the standard deviation. Compare the result to the standard deviation computed using all of the data.
Body Temperatures Refer to Data Set 5 “Body Temperatures” in Appendix B and use the body temperatures for 12:00 AM on day 2.
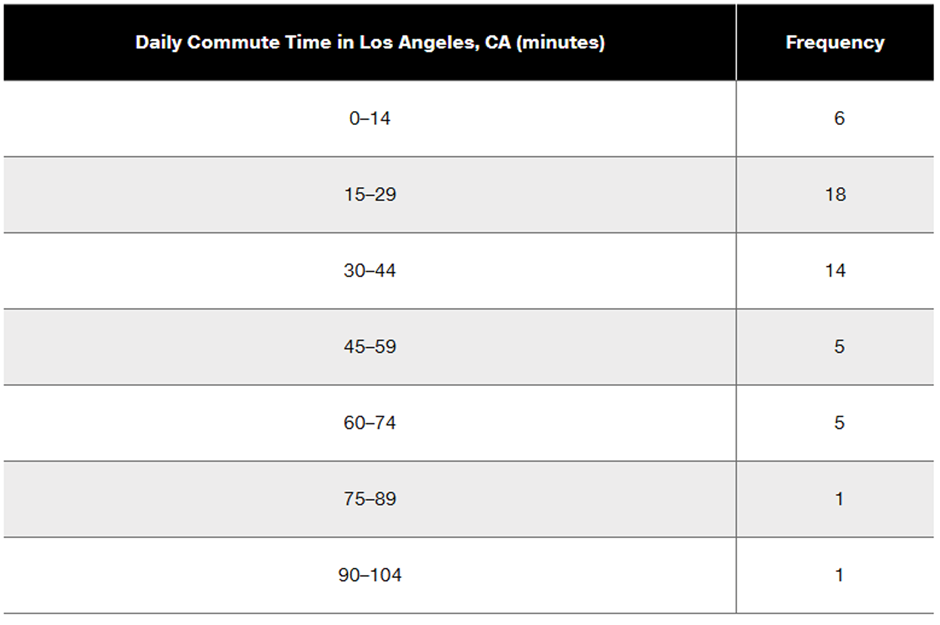
Problem 3.2.37
Finding Standard Deviation from a Frequency Distribution. In Exercises 37–40, refer to the frequency distribution in the given exercise and compute the standard deviation by using the formula below, where x represents the class midpoint, f represents the class frequency, and n represents the total number of sample values. Also, compare the computed standard deviations to these standard deviations obtained by using Formula 3-4 with the original list of data values: (Exercise 37) 18.5 minutes; (Exercise 38) 36.7 minutes; (Exercise 39) 6.9 years; (Exercise 40) 20.4 seconds.
Standard deviation for frequency distribution
Problem 3.2.41
The Empirical Rule Based on Data Set 1 “Body Data” in Appendix B, blood platelet counts of women have a bell-shaped distribution with a mean of 255.1 and a standard deviation of 65.4. (All units are 1000 cells/) Using the empirical rule, what is the approximate percentage of women with platelet counts
a. within 2 standard deviations of the mean, or between 124.3 and 385.9?
Problem 3.2.45
Why Divide by ? Let a population consist of the values 9 cigarettes, 10 cigarettes, and 20 cigarettes smoked in a day (based on data from the California Health Interview Survey). Assume that samples of two values are randomly selected with replacement from this population. (That is, a selected value is replaced before the second selection is made.)
a. Find the variance of the population {9 cigarettes, 10 cigarettes, 20 cigarettes}.
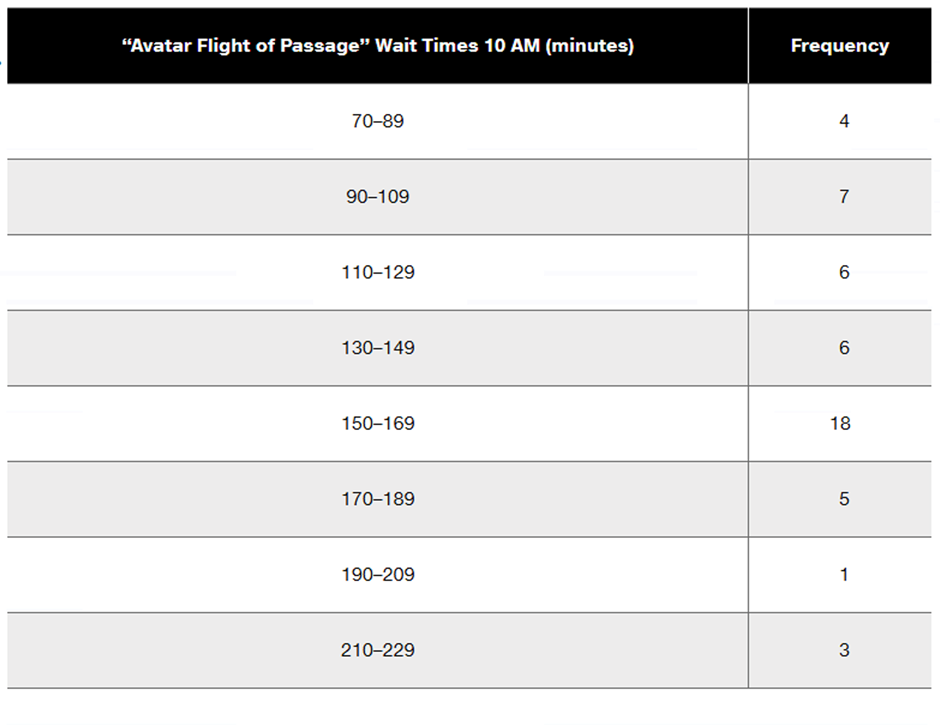
Problem 3.2.38
Finding Standard Deviation from a Frequency Distribution. In Exercises 37–40, refer to the frequency distribution in the given exercise and compute the standard deviation by using the formula below, where x represents the class midpoint, f represents the class frequency, and n represents the total number of sample values. Also, compare the computed standard deviations to these standard deviations obtained by using Formula 3-4 with the original list of data values: (Exercise 37) 18.5 minutes; (Exercise 38) 36.7 minutes; (Exercise 39) 6.9 years; (Exercise 40) 20.4 seconds.
Standard deviation for frequency distribution
Problem 3.2.45b
Why Divide by ? Let a population consist of the values 9 cigarettes, 10 cigarettes, and 20 cigarettes smoked in a day (based on data from the California Health Interview Survey). Assume that samples of two values are randomly selected with replacement from this population. (That is, a selected value is replaced before the second selection is made.)
b. After listing the nine different possible samples of two values selected with replacement, find the sample variance (which includes division by ) for each of them; then find the mean of the nine sample variances s2.
Problem 3.2.45c
Why Divide by ? Let a population consist of the values 9 cigarettes, 10 cigarettes, and 20 cigarettes smoked in a day (based on data from the California Health Interview Survey). Assume that samples of two values are randomly selected with replacement from this population. (That is, a selected value is replaced before the second selection is made.)
c. For each of the nine different possible samples of two values selected with replacement, find the variance by treating each sample as if it is a population (using the formula for population variance, which includes division by n); then find the mean of those nine population variances.
Problem 3.2.45d
Why Divide by ? Let a population consist of the values 9 cigarettes, 10 cigarettes, and 20 cigarettes smoked in a day (based on data from the California Health Interview Survey). Assume that samples of two values are randomly selected with replacement from this population. (That is, a selected value is replaced before the second selection is made.)
d. Which approach results in values that are better estimates of part (b) or part (c)? Why? When computing variances of samples, should you use division by n or
Problem 3.2.46
Mean Absolute Deviation Use the same population of {9 cigarettes, 10 cigarettes, 20 cigarettes} from Exercise 45. Show that when samples of size 2 are randomly selected with replacement, the samples have mean absolute deviations that do not center about the value of the mean absolute deviation of the population. What does this indicate about a sample mean absolute deviation being used as an estimator of the mean absolute deviation of a population?
Problem 3.3.33
Boxplots from Large Data Sets in Appendix B. In Exercises 33–36, use the given data sets in Appendix B. Use the boxplots to compare the two data sets.
Pulse Rates Use the same scale to construct boxplots for the pulse rates of males and females from Data Set 1 “Body Data” in Appendix B.
Problem 3.3.32
Boxplots. In Exercises 29–32, use the given data to construct a boxplot and identify the 5-number summary.
Blood Pressure Measurements Fourteen different second-year medical students at Bellevue Hospital measured the blood pressure of the same person. The systolic readings (mm Hg) are listed below.
138 130 135 140 120 125 120 130 130 144 143 140 130 150
Problem 3.3.30
Boxplots. In Exercises 29–32, use the given data to construct a boxplot and identify the 5-number summary.
Taxis Listed below are times (minutes) of a sample of taxi rides in New York City. The data are from the New York City Taxi and Limousine Commission.
15 12 31 3 11 33 62 4
Problem 3.3.13
Comparing Values. In Exercises 13–16, use z scores to compare the given values.
Tallest and Shortest Men The tallest adult male was Robert Wadlow, and his height was 272 cm. The shortest adult male was Chandra Bahadur Dangi, and his height was 54.6 cm. Heights of men have a mean of 174.12 cm and a standard deviation of 7.10 cm. Which of these two men has the height that is more extreme?
Problem 3.3.10
Significant Values. In Exercises 9–12, use the range rule of thumb to identify (a) the values that are significantly low, (b) the values that are significantly high, and (c) the values that are neither significantly low nor significantly high.
IQ Scores The Wechsler test is used to measure intelligence of adults aged 16 to 80. The mean test score is 100 and the standard deviation is 15.
Problem 3.3.17
Percentiles. In Exercises 17–20, use the following radiation levels (in W/kg) for 50 different cell phones. Find the percentile corresponding to the given radiation level.
0.48 W/kg
Problem 3.3.18
Percentiles. In Exercises 17–20, use the following radiation levels (in W/kg) for 50 different cell phones. Find the percentile corresponding to the given radiation level.
1.47 W/kg
Problem 3.3.21
In Exercises 21–28, use the same list of cell phone radiation levels given for Exercises 17–20. Find the indicated percentile or quartile.
P30
Problem 3.3.22
In Exercises 21–28, use the same list of cell phone radiation levels given for Exercises 17–20. Find the indicated percentile or quartile.
Q1
Problem 3.3.23
In Exercises 21–28, use the same list of cell phone radiation levels given for Exercises 17–20. Find the indicated percentile or quartile.
Q3
Problem 3.3.25
In Exercises 21–28, use the same list of cell phone radiation levels given for Exercises 17–20. Find the indicated percentile or quartile.
P50
Problem 3.3.4
z Scores If your score on your next statistics test is converted to a z score, which of these z scores would you prefer: -2.00, -1.00, 0, 1.00, 2.00? Why?
Problem 3.3.5a
z Scores. In Exercises 5–8, express all z scores with two decimal places.
Diastolic Blood Pressure of Females For the diastolic blood pressure measurements of females listed in Data Set 1 “Body Data” in Appendix B, the highest measurement is 98 mm Hg. The 147 diastolic blood pressure measurements of females have a mean of 70.2 mm Hg and a standard deviation of 11.2 mm Hg.
a. What is the difference between the highest diastolic blood pressure and the mean of the diastolic blood pressures for females?