"Finding a Critical F-Value for a Right-Tailed Test In Exercises 5 – 8, find the critical F-value for a right-tailed test using the level of significance α and degrees of freedom d.f.N and d.f.D.

α=0.05, d.f.N=9, d.f.D=16"

"Finding a Critical F-Value for a Right-Tailed Test In Exercises 5 – 8, find the critical F-value for a right-tailed test using the level of significance α and degrees of freedom d.f.N and d.f.D.

α=0.01, d.f.N=2, d.f.D=11"

"Finding a Critical F-Value for a Right-Tailed Test In Exercises 5 – 8, find the critical F-value for a right-tailed test using the level of significance α and degrees of freedom d.f.N and d.f.D.

α=0.025, d.f.N=7, d.f.D=3"

"Finding a Critical F-Value for a Two-Tailed Test In Exercises 9 –12, find the critical F-value for a two-tailed test using the level of significance α and degrees of freedom d.f.N and d.f.D.

α=0.10, d.f.N=24, d.f.D=28"

"Finding a Critical F-Value for a Two-Tailed Test In Exercises 9 –12, find the critical F-value for a two-tailed test using the level of significance α and degrees of freedom d.f.N and d.f.D.

α=0.05, d.f.N=60, d.f.D=40"

"Finding a Critical F-Value for a Two-Tailed Test In Exercises 9 –12, find the critical F-value for a two-tailed test using the level of significance α and degrees of freedom d.f.N and d.f.D.

α=0.05, d.f.N=27, d.f.D=19"

"In Exercises 13 –18, test the claim about the difference between two population variances σ₁² and σ₂² at the level of significance α. Assume the samples are random and independent, and the populations are normally distributed.

Claim: σ₁² > σ₂²; α = 0.10.

Sample statistics: s₁² = 773, n₁ = 5 and s₂² = 765, n₂ = 6"

"In Exercises 13 –18, test the claim about the difference between two population variances σ₁² and σ₂² at the level of significance α. Assume the samples are random and independent, and the populations are normally distributed.

Claim: σ₁² = σ₂²; α = 0.05.

Sample statistics: s₁² = 310, n₁ = 7 and s₂² = 297, n₂ = 8"

"Performing a Two-Sample F-Test In Exercises 19 –26, (a) identify the claim and state H0 and Ha, (b) find the critical value and identify the rejection region, (c) find the test statistic F, (d) decide whether to reject or fail to reject the null hypothesis, and (e) interpret the decision in the context of the original claim. Assume the samples are random and independent, and the populations are normally distributed.

Life of Appliances Company A claims that the variance of the lives of its appliances is less than the variance of the lives of Company B’s appliances. A sample of the lives of 20 of Company A’s appliances has a variance of 1.8. A sample of the lives of 25 of Company B’s appliances has a variance of 3.9. At α=0.025, can you support Company A’s claim?"

"Performing a Two-Sample F-Test In Exercises 19 –26, (a) identify the claim and state H0 and Ha, (b) find the critical value and identify the rejection region, (c) find the test statistic F, (d) decide whether to reject or fail to reject the null hypothesis, and (e) interpret the decision in the context of the original claim. Assume the samples are random and independent, and the populations are normally distributed.

Carbon Monoxide Emissions An automobile manufacturer claims that the variance of the carbon monoxide emissions for a make and model of one of its vehicles is less than the variance of the carbon monoxide emissions for a top competitor’s equivalent vehicle. A sample of the carbon monoxide emissions of 19 of the manufacturer’s specified vehicles has a variance of 0.008. A sample of the carbon monoxide emissions of 21 of its competitor’s equivalent vehicles has a variance of 0.045. At α=0.10, can you support the manufacturer’s claim? (Adapted from U.S. Environmental Protection Agency)"

"Finding Left-Tailed Critical F-Values In this section, you only needed to calculate the right-tailed critical F-value for a two-tailed test. For other applications of the F-distribution, you will need to calculate the left-tailed critical F-value. To calculate the left-tailed critical F-value, perform the steps below.

1. Interchange the values for d.f.N and d.f.D.

2. Find the corresponding F-value in Table 7.

3. Calculate the reciprocal of the F-value to obtain the left-tailed critical F-value.

In Exercises 27 and 28, find the right- and left-tailed critical F-values for a two-tailed test using the level of significance α and degrees of freedom d.f.N and d.f.D.

α=0.10, d.f.N=20, d.f.D=15"

State the null and alternative hypotheses for a one-way ANOVA test.

What conditions are necessary in order to use a one-way ANOVA test?

Describe the difference between the variance between samples MSB and the variance within samples MSW.

Describe the hypotheses for a two-way ANOVA test.

Performing a One-Way ANOVA Test In Exercises 5 –14, (a) identify the claim and state H0 and Ha, (b) find the critical value and identify the rejection region, (c) find the test statistic F, (d) decide whether to reject or fail to reject the null hypothesis, and (e) interpret the decision in the context of the original claim. Assume the samples are random and independent, the populations are normally distributed, and the population variances are equal.

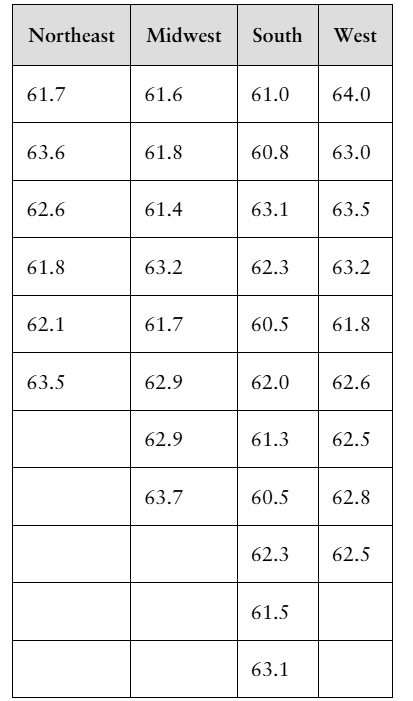
[APPLET] Well-Being Index The well-being index is a way to measure how people are faring physically, emotionally, socially, and professionally, as well as to rate the overall quality of their lives and their outlooks for the future. The table shows the well-being index scores for a sample of states from four regions of the United States. At α=0.10, can you reject the claim that the mean score is the same for all regions? (Adapted from Gallup and Healthways)

Performing a One-Way ANOVA Test In Exercises 5 –14, (a) identify the claim and state H0 and Ha, (b) find the critical value and identify the rejection region, (c) find the test statistic F, (d) decide whether to reject or fail to reject the null hypothesis, and (e) interpret the decision in the context of the original claim. Assume the samples are random and independent, the populations are normally distributed, and the population variances are equal.

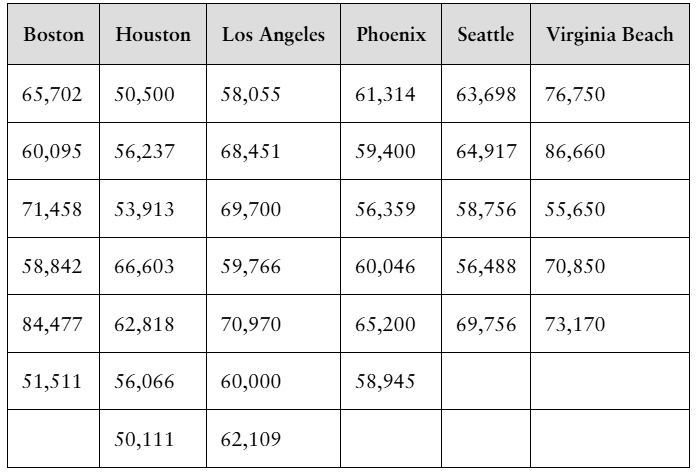
[APPLET] Statistician Salaries The table shows the salaries of a sample of entry level statisticians from six large metropolitan areas. At α=0.05, can you conclude that the mean salary is different in at least one of the areas? (Adapted from Salary.com)

"Using Technology to Perform a Two-Way ANOVA Test In Exercises 15 –18, use technology and the block design to perform a two-way ANOVA test. Use α=0.10. Interpret the results. Assume the samples are random and independent, the populations are normally distributed, and the population variances are equal.

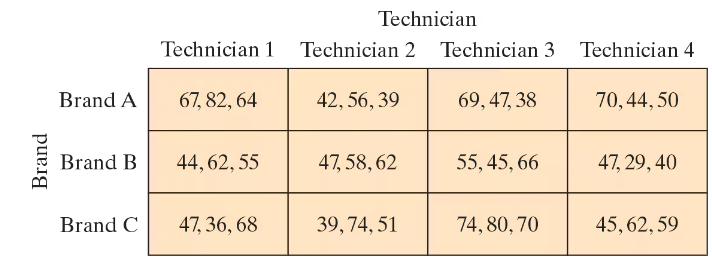
[APPLET] Laptop Repairs The manager of a computer repair service wants to determine whether there is a difference in the time it takes four technicians to repair different brands of laptops. The block design shows the times (in minutes) it took for each technician to repair three laptops of each brand.

List the two conditions that must be met in order to use the paired-sample sign test.