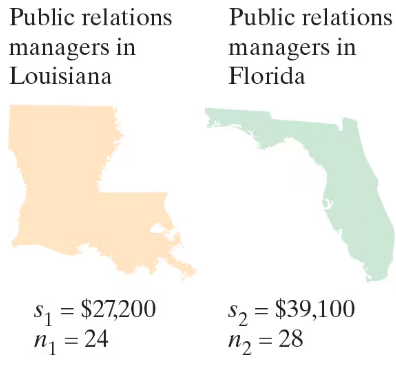Explain why the chi-square independence test is always a right-tailed test.

True or False? In Exercises 5 and 6, determine whether the statement is true or false. If it is false, rewrite it as a true statement.

If the two variables in a chi-square independence test are dependent, then you can expect little difference between the observed frequencies and the expected frequencies.

True or False? In Exercises 5 and 6, determine whether the statement is true or false. If it is false, rewrite it as a true statement.

When the test statistic for the chi-square independence test is large, you will, in most cases, reject the null hypothesis.

Finding Expected Frequencies

In Exercises 7–12, (a) calculate the marginal frequencies and (b) find the expected frequency for each cell in the contingency table. Assume that the variables are independent.

Finding Expected Frequencies

In Exercises 7–12, (a) calculate the marginal frequencies and (b) find the expected frequency for each cell in the contingency table. Assume that the variables are independent.

Performing a Chi-Square Independence Test In Exercises 13–28, perform the indicated chi-square independence test by performing the steps below.

a. Identify the claim and state H₀ and Hₐ

b. Determine the degrees of freedom, find the critical value, and identify the rejection region.

c. Find the chi-square test statistic.

d. Decide whether to reject or fail to reject the null hypothesis.

e. Interpret the decision in the context of the original claim.

Use the contingency table and expected frequencies from Exercise 8. At α=0.05, test the hypothesis that the variables are dependent.

Performing a Chi-Square Independence Test In Exercises 13–28, perform the indicated chi-square independence test by performing the steps below.

a. Identify the claim and state H₀ and Hₐ

b. Determine the degrees of freedom, find the critical value, and identify the rejection region.

c. Find the chi-square test statistic.

d. Decide whether to reject or fail to reject the null hypothesis.

e. Interpret the decision in the context of the original claim.

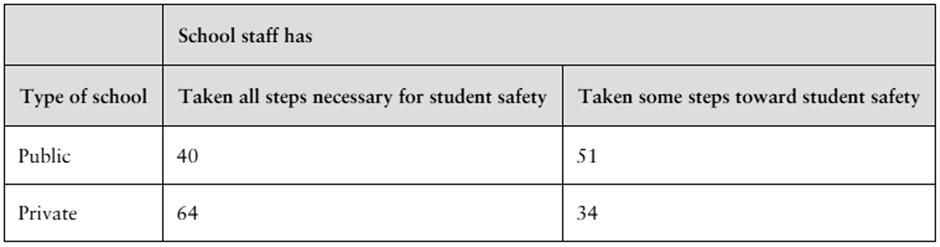
Attitudes about Safety The contingency table shows the results of a random sample of students by type of school and their attitudes on safety steps taken by the school staff. At α=0.01, can you conclude that attitudes about the safety steps taken by the school staff are related to the type of school? (Adapted from Horatio Alger Association)

Performing a Chi-Square Independence Test In Exercises 13–28, perform the indicated chi-square independence test by performing the steps below.

a. Identify the claim and state H₀ and Hₐ

b. Determine the degrees of freedom, find the critical value, and identify the rejection region.

c. Find the chi-square test statistic.

d. Decide whether to reject or fail to reject the null hypothesis.

e. Interpret the decision in the context of the original claim.

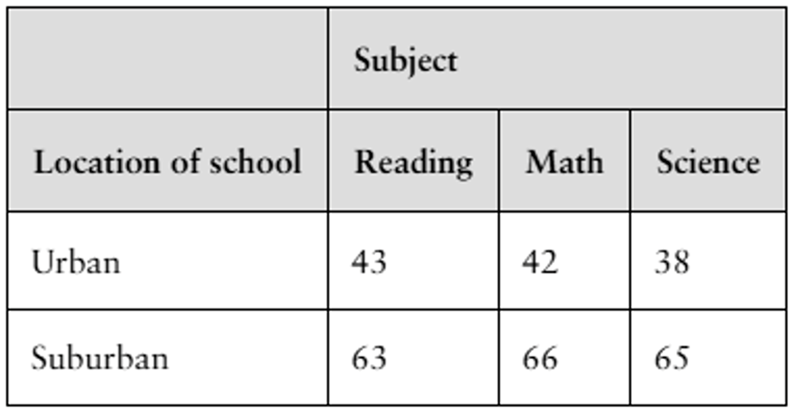
Achievement and School Location The contingency table shows the results of a random sample of students by the location of school and the number of those students achieving basic skill levels in three subjects. At α=0.01, test the hypothesis that the variables are independent. (Adapted from HUD State of the Cities Report)

Performing a Chi-Square Independence Test In Exercises 13–28, perform the indicated chi-square independence test by performing the steps below.

a. Identify the claim and state H₀ and Hₐ

b. Determine the degrees of freedom, find the critical value, and identify the rejection region.

c. Find the chi-square test statistic.

d. Decide whether to reject or fail to reject the null hypothesis.

e. Interpret the decision in the context of the original claim.

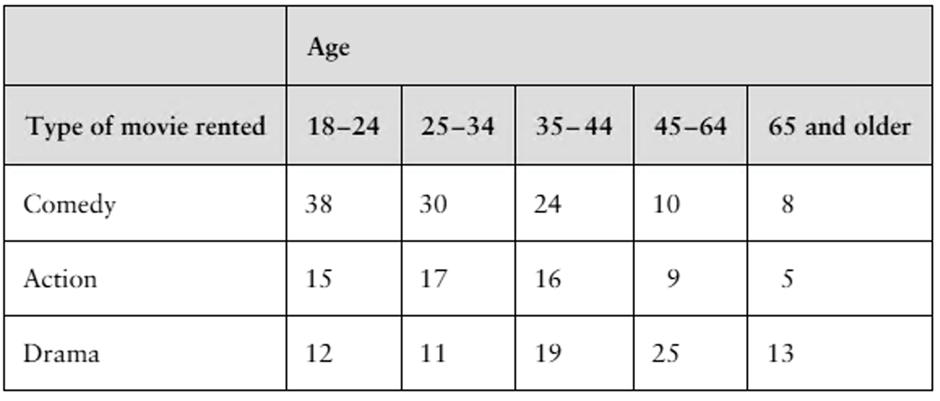
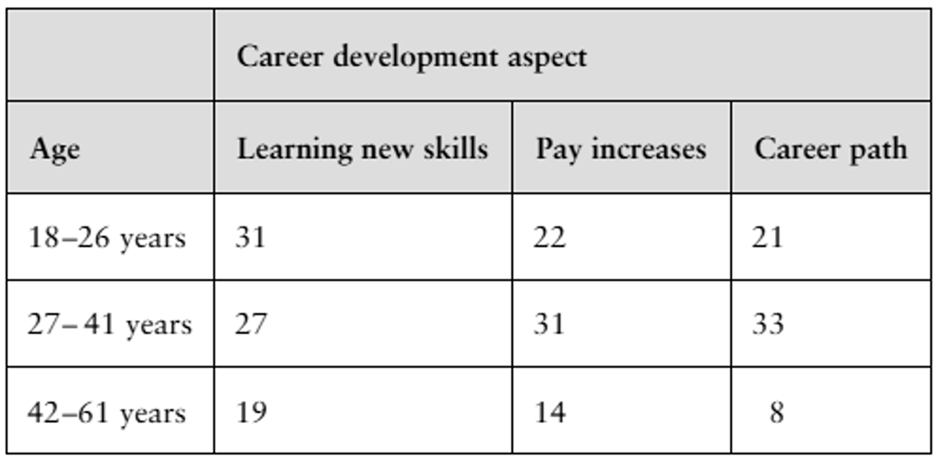
Ages and Goals You are investigating the relationship between the ages of U.S. adults and what aspect of career development they consider to be the most important. You randomly collect the data shown in the contingency table. At α=0.10, is there enough evidence to conclude that age is related to which aspect of career development is considered to be most important? (Adapted from The Harris Poll)

Contingency Tables and Relative Frequencies In Exercises 33–36, use the information below.

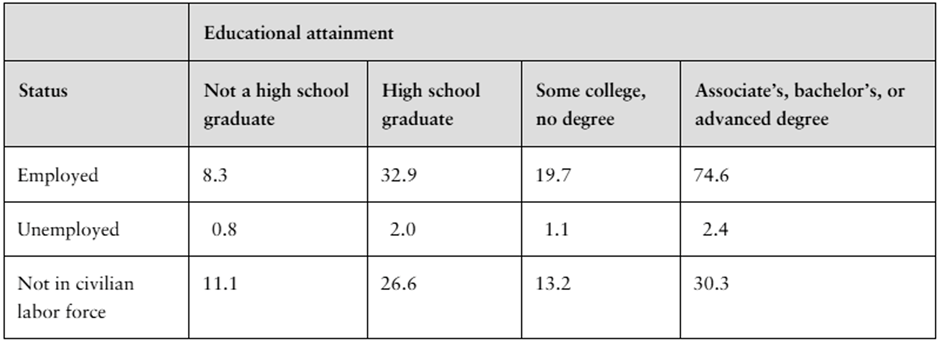
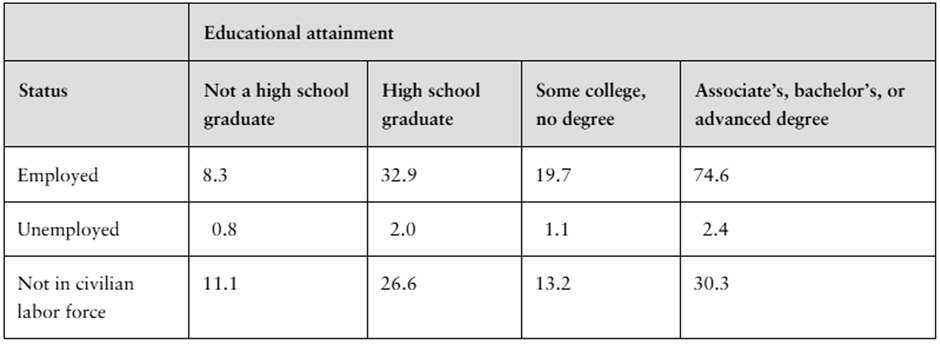
The frequencies in a contingency table can be written as relative frequencies by dividing each frequency by the sample size. The contingency table below shows the number of U.S. adults (in millions) ages 25 and over by employment status and educational attainment. (Adapted from U.S. Census Bureau)

Explain why you cannot perform the chi-square independence test on these data.

Contingency Tables and Relative Frequencies In Exercises 33–36, use the information below.

The frequencies in a contingency table can be written as relative frequencies by dividing each frequency by the sample size. The contingency table below shows the number of U.S. adults (in millions) ages 25 and over by employment status and educational attainment. (Adapted from U.S. Census Bureau)

What percent of U.S. adults ages 25 and over (a) are employed and are only high school graduates, (b) are not in the civilian labor force, and (c) are not high school graduates?

Conditional Relative Frequencies In Exercises 37 –42, use the contingency table from Exercises 33–36, and the information below.

Relative frequencies can also be calculated based on the row totals (by dividing each row entry by the row’s total) or the column totals (by dividing each column entry by the column’s total). These frequencies are conditional relative frequencies and can be used to determine whether an association exists between two categories in a contingency table.

What percent of U.S. adults ages 25 and over who are employed have a degree?

Conditional Relative Frequencies In Exercises 37 –42, use the contingency table from Exercises 33–36, and the information below.

Relative frequencies can also be calculated based on the row totals (by dividing each row entry by the row’s total) or the column totals (by dividing each column entry by the column’s total). These frequencies are conditional relative frequencies and can be used to determine whether an association exists between two categories in a contingency table.

What percent of U.S. adults ages 25 and over who have a degree are not in the civilian labor force?

Conditional Relative Frequencies In Exercises 37 –42, use the contingency table from Exercises 33–36, and the information below.

Relative frequencies can also be calculated based on the row totals (by dividing each row entry by the row’s total) or the column totals (by dividing each column entry by the column’s total). These frequencies are conditional relative frequencies and can be used to determine whether an association exists between two categories in a contingency table.

What percent of U.S. adults ages 25 and over who are not high school graduates are unemployed?

Performing a Chi-Square Independence Test In Exercises 13–28, perform the indicated chi-square independence test by performing the steps below.

a. Identify the claim and state H₀ and Hₐ

b. Determine the degrees of freedom, find the critical value, and identify the rejection region.

c. Find the chi-square test statistic.

d. Decide whether to reject or fail to reject the null hypothesis.

e. Interpret the decision in the context of the original claim.

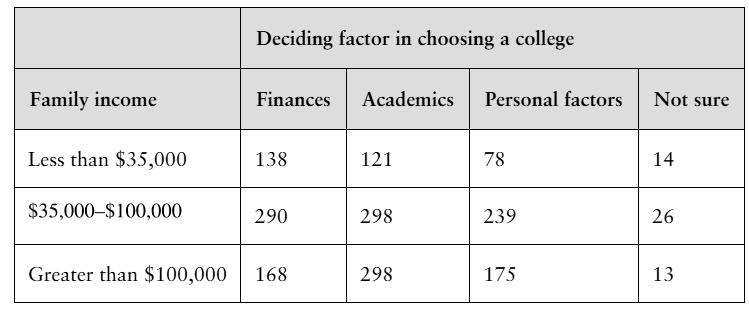
Choosing a College The contingency table shows the results of a survey asking 1858 parents and students of different incomes what their deciding factor was in choosing a college. At α=0.01, can you conclude that the deciding factor in choosing a college is related to the income of the family? (Adapted from Sallie Mae)

Performing a Chi-Square Independence Test In Exercises 13–28, perform the indicated chi-square independence test by performing the steps below.

a. Identify the claim and state H₀ and Hₐ

b. Determine the degrees of freedom, find the critical value, and identify the rejection region.

c. Find the chi-square test statistic.

d. Decide whether to reject or fail to reject the null hypothesis.

e. Interpret the decision in the context of the original claim.

Use the contingency table and expected frequencies from Exercise 11. At α=0.10, test the hypothesis that the variables are independent.

Performing a Chi-Square Independence Test In Exercises 13–28, perform the indicated chi-square independence test by performing the steps below.

a. Identify the claim and state H₀ and Hₐ

b. Determine the degrees of freedom, find the critical value, and identify the rejection region.

c. Find the chi-square test statistic.

d. Decide whether to reject or fail to reject the null hypothesis.

e. Interpret the decision in the context of the original claim.

Use the contingency table and expected frequencies from Exercise 10. At α=0.01, test the hypothesis that the variables are dependent.

Performing a Chi-Square Independence Test In Exercises 13–28, perform the indicated chi-square independence test by performing the steps below.

a. Identify the claim and state H₀ and Hₐ

b. Determine the degrees of freedom, find the critical value, and identify the rejection region.

c. Find the chi-square test statistic.

d. Decide whether to reject or fail to reject the null hypothesis.

e. Interpret the decision in the context of the original claim.

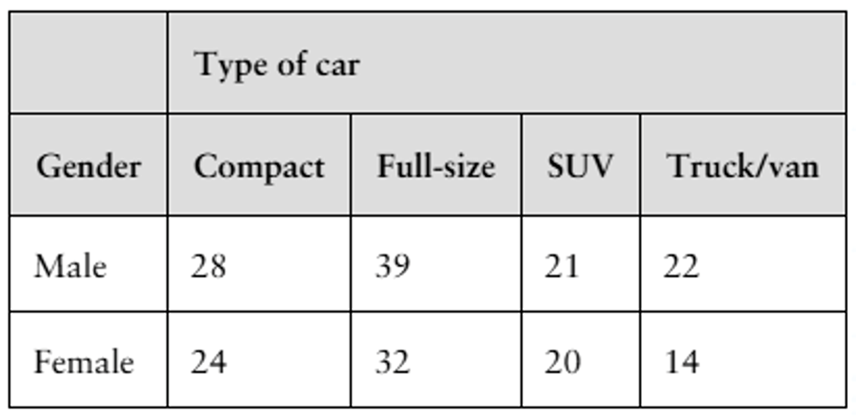
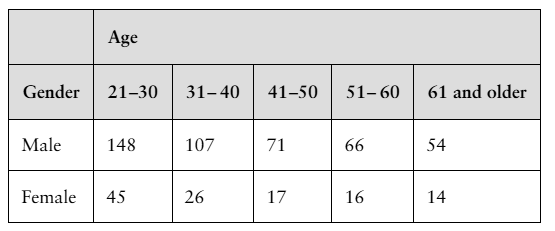
Alcohol-Related Accidents The contingency table shows the results of a random sample of fatally injured passenger vehicle drivers (with blood alcohol concentrations greater than or equal to 0.08) by age and gender. At α=0.05, can you conclude that age is related to gender in such alcohol-related accidents? (Adapted from Insurance Institute for Highway Safety)

Finding a Critical F-Value for a Right-Tailed Test In Exercises 5 – 8, find the critical F-value for a right-tailed test using the level of significance α and degrees of freedom d.f.N and d.f.D.

α=0.10, d.f.N=10, d.f.D=15

Finding a Critical F-Value for a Two-Tailed Test In Exercises 9 –12, find the critical F-value for a two-tailed test using the level of significance α and degrees of freedom d.f.N and d.f.D.

α=0.01, d.f.N=6, d.f.D=7

In Exercises 13 –18, test the claim about the difference between two population variances σ₁² and σ₂² at the level of significance α. Assume the samples are random and independent, and the populations are normally distributed.

Claim: σ₁² ≤ σ₂²; α = 0.01.

Sample statistics: s₁² = 842, n₁ = 11 and s₂² = 836, n₂ = 10

In Exercises 13 –18, test the claim about the difference between two population variances σ₁² and σ₂² at the level of significance α. Assume the samples are random and independent, and the populations are normally distributed.

Claim: σ₁² ≠ σ₂²; α = 0.05.

Sample statistics: s₁² = 245, n₁ = 31 and s₂² = 112, n₂ = 28

In Exercises 13 –18, test the claim about the difference between two population variances σ₁² and σ₂² at the level of significance α. Assume the samples are random and independent, and the populations are normally distributed.

Claim: σ₁² > σ₂²; α = 0.05.

Sample statistics: s₁² = 44.6, n₁ = 16 and s₂² = 39.3, n₂ = 12

Performing a Two-Sample F-Test In Exercises 19 –26, (a) identify the claim and state H0 and Ha, (b) find the critical value and identify the rejection region, (c) find the test statistic F, (d) decide whether to reject or fail to reject the null hypothesis, and (e) interpret the decision in the context of the original claim. Assume the samples are random and independent, and the populations are normally distributed.

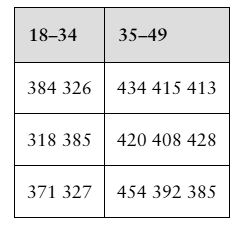
Heart Transplant Waiting Times The table at the left shows a sample of the waiting times (in days) for a heart transplant for two age groups. At α=0.05, can you conclude that the variances of the waiting times differ between the two age groups? (Adapted from Organ Procurement and Transplantation Network)

Performing a Two-Sample F-Test In Exercises 19 –26, (a) identify the claim and state H0 and Ha, (b) find the critical value and identify the rejection region, (c) find the test statistic F, (d) decide whether to reject or fail to reject the null hypothesis, and (e) interpret the decision in the context of the original claim. Assume the samples are random and independent, and the populations are normally distributed.

U.S. History Assessment Tests A state school administrator claims that the standard deviations of U.S. history assessment test scores for eighth-grade students are the same in Districts 1 and 2. A sample of 10 test scores from District 1 has a standard deviation of 30.9 points, and a sample of 13 test scores from District 2 has a standard deviation of 27.2 points. At α=0.01, can you reject the administrator’s claim? (Adapted from National Center for Education Statistics)

Performing a Two-Sample F-Test In Exercises 19 –26, (a) identify the claim and state H0 and Ha, (b) find the critical value and identify the rejection region, (c) find the test statistic F, (d) decide whether to reject or fail to reject the null hypothesis, and (e) interpret the decision in the context of the original claim. Assume the samples are random and independent, and the populations are normally distributed.

Annual Salaries An employment information service claims that the standard deviation of the annual salaries for public relations managers is less in Louisiana than in Florida. You select a sample of public relations managers from each state. The results of each survey are shown in the figure. At α=0.05, can you support the service’s claim? (Adapted from America’s Career InfoNet)

Explain how to find the critical value for an F-test.

List five properties of the F-distribution.

List the three conditions that must be met in order to use a two-sample F-test.

Explain how to determine the values of d.f.N and d.f.D when performing a two-sample F-test.