Open Question
a
1. Intro to Stats and Collecting Data
Intro to Stats
3:14 minutesProblem 1.1.17
Textbook Question
In Exercises 13–20, determine whether the results appear to have statistical significance, and also determine whether the results appear to have practical significance.
Election Fraud The County Clerk in Essex County, New Jersey, was responsible for randomly assigning the order in which candidates’ names appeared on a recent election ballot. Among 41 different ballots, a Democrat was placed on the first line 40 times, and a Republican was placed on the first line once.
Verified step by step guidance1
Step 1: Define statistical significance. Statistical significance refers to the likelihood that a result or relationship is caused by something other than mere random chance. In this context, we need to determine if the observed distribution of candidates on the first line is unlikely to occur by random chance.
Step 2: Set up the null hypothesis. The null hypothesis typically states that there is no effect or no difference. Here, it would be that the placement of candidates on the first line is random, meaning each candidate has an equal chance of being placed first.
Step 3: Calculate the expected frequency under the null hypothesis. If the placement is random, each candidate (Democrat or Republican) should appear on the first line approximately half the time. With 41 ballots, the expected frequency for each party would be 20.5 times.
Step 4: Perform a statistical test. Use a chi-square test for goodness of fit to compare the observed frequencies (40 Democrats, 1 Republican) with the expected frequencies (20.5 Democrats, 20.5 Republicans). Calculate the chi-square statistic using the formula: , where O is the observed frequency and E is the expected frequency.
Step 5: Determine practical significance. Even if the result is statistically significant, consider whether it has practical significance. Practical significance refers to whether the result has real-world implications or importance. In this case, consider the impact of having one party consistently listed first on the ballot and whether it could influence voter behavior.
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
3mWas this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Statistical Significance
Statistical significance refers to the likelihood that a result or relationship is caused by something other than mere random chance. In the context of the election fraud question, it involves determining if the observed pattern of ballot placements is unlikely under a fair random assignment, typically using a p-value to assess this probability.
Recommended video:
Guided course
06:34
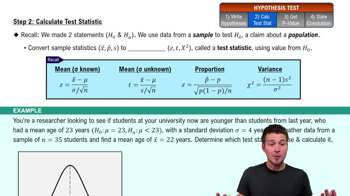
Step 2: Calculate Test Statistic
Practical Significance
Practical significance considers whether a statistically significant result has real-world implications or importance. Even if the ballot placement pattern is statistically significant, practical significance asks whether this pattern affects the election outcome or voter behavior in a meaningful way, beyond just being statistically unusual.
Recommended video:
Guided course
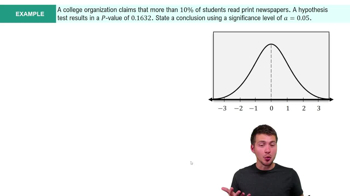
04:46Step 4: State Conclusion Example 4
Random Assignment
Random assignment is a process used to ensure that each candidate has an equal chance of being placed in any position on the ballot. In this scenario, understanding random assignment is crucial to evaluating whether the observed pattern of ballot placements deviates from what would be expected under fair conditions, thus indicating potential bias or manipulation.
Recommended video:
Guided course
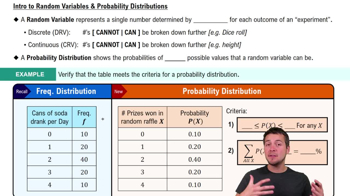
07:09Intro to Random Variables & Probability Distributions
2:13mWatch next
Master Introduction to Statistics Channel with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice