7. Sampling Distributions & Confidence Intervals: Mean

Confidence Intervals for Population Mean

7. Sampling Distributions & Confidence Intervals: Mean

Confidence Intervals for Population Mean

2:25 minutes

Problem 7.CQQ.7

Textbook Question

Requirements A construction quality control analyst has collected a random sample of six concrete road barriers, and she plans to weigh each of them and construct a 95% confidence interval estimate of the mean weight of all such barriers. What requirements must be satisfied in order to construct the confidence interval with the method from Section 7-2 that uses the t distribution?

Verified step by step guidance

Verify that the sample is a simple random sample. This means the six concrete road barriers must have been selected randomly from the population of all such barriers, ensuring that each barrier had an equal chance of being included in the sample.

Check that the population of weights of all concrete road barriers is approximately normally distributed. If the population distribution is not known, this assumption can be relaxed if the sample size is sufficiently large (typically n > 30), but since the sample size here is only 6, normality is important.

Ensure that the sample size is small relative to the population size. Specifically, the sample size (n = 6) should not exceed 5% of the total population of concrete road barriers. This ensures independence between sampled observations.

Confirm that the population standard deviation is unknown. The t-distribution method is used when the population standard deviation is not known, and the sample standard deviation is used as an estimate.

Verify that the data does not contain significant outliers. Outliers can heavily influence the mean and standard deviation, which would affect the accuracy of the confidence interval. Use visual tools like boxplots or statistical tests to check for outliers.

Verified video answer for a similar problem:

This video solution was recommended by our tutors as helpful for the problem above

Video duration:

Was this helpful?

Key Concepts

Here are the essential concepts you must grasp in order to answer the question correctly.

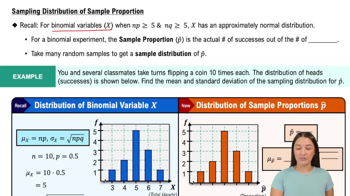
Random Sampling

Random sampling is a fundamental concept in statistics that ensures each member of a population has an equal chance of being selected. This method helps to eliminate bias and allows for the generalization of results from the sample to the entire population. In the context of the question, the analyst's use of a random sample of six concrete road barriers is crucial for the validity of the confidence interval.

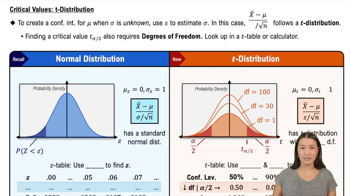
t Distribution

The t distribution is a type of probability distribution that is used when estimating population parameters when the sample size is small (typically less than 30) and the population standard deviation is unknown. It is similar to the normal distribution but has heavier tails, which accounts for the increased variability expected in smaller samples. The use of the t distribution is essential for constructing confidence intervals in this scenario.

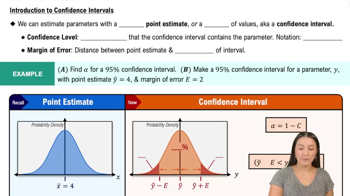
Confidence Interval

A confidence interval is a range of values, derived from a sample, that is likely to contain the population parameter with a specified level of confidence, such as 95%. It provides an estimate of uncertainty around the sample mean and is calculated using the sample mean, the t statistic, and the standard error. Understanding how to construct and interpret confidence intervals is key to making inferences about the population based on sample data.

Watch next

Master Population Standard Deviation Known with a bite sized video explanation from Patrick

Start learning

Related Videos

Related Practice

Textbook Question

Los Angeles Commute Time Listed below are 15 Los Angeles commute times (based on a sample from Data Set 31 “Commute Times” in Appendix B). Construct a 99% confidence interval estimate of the population mean. Is the confidence interval a good estimate of the population mean?

Textbook Question

Genes Samples of DNA are collected, and the four DNA bases of A, G, C, and T are coded as 1, 2, 3, and 4, respectively. The results are listed below. Construct a 95% confidence interval estimate of the mean. What is the practical use of the confidence interval?

2 2 1 4 3 3 3 3 4 1

Textbook Question

Mercury in Sushi An FDA guideline is that the mercury in fish should be below 1 part per million (ppm). Listed below are the amounts of mercury (ppm) found in tuna sushi sampled at different stores in New York City. The study was sponsored by the New York Times, and the stores (in order) are D’Agostino, Eli’s Manhattan, Fairway, Food Emporium, Gourmet Garage, Grace’s Marketplace, and Whole Foods. Construct a 98% confidence interval estimate of the mean amount of mercury in the population. Does it appear that there is too much mercury in tuna sushi?

0.56 0.75 0.10 0.95 1.25 0.54 0.88

Textbook Question

Quarters Assume that weights of quarters minted after 1964 are normally distributed with a mean of 5.670 g and a standard deviation of 0.062 g (based on U.S. Mint specifications).

b. If 25 quarters are randomly selected, find the probability that their mean weight is greater than 5.675 g.

Textbook Question

Degrees of Freedom In general, what does “degrees of freedom” refer to? For the sample data described in Exercise 7 “Requirements,” find the number of degrees of freedom, assuming that you want to construct a confidence interval estimate of u using the t distribution.

Textbook Question

Space Mountain Use the following wait times (minutes) for the Space Mountain ride at Disney World (from Data Set 33 “Disney World Wait Times” in Appendix B). Construct a 95% confidence interval estimate of the mean of all wait times. Write a brief statement that interprets that confidence interval.

40 35 40 40 25 80 50 30 35 40

Textbook Question

In Exercises 1–4, refer to the accompanying screen display that results from a simple random sample of times (minutes) between eruptions of the Old Faithful geyser. The confidence level of 95% was used.

Refer to the accompanying screen display.

a. Express the confidence interval in the format that uses the “less than” symbol. Round the confidence interval limits given that the original times are all rounded to one decimal place.

Textbook Question

Degrees of Freedom

a. What is the number of degrees of freedom that should be used for finding the critical value ta/2?

Show more practices