A personal trainer is studying whether a new stretching routine improves flexibility. She records the forward reach (in cm) of 6 clients before and after a 4-week program. Calculate the difference (after - before) for each client, the mean difference, and standard deviation.
Table of contents
- 1. Intro to Stats and Collecting Data1h 14m
- 2. Describing Data with Tables and Graphs1h 55m
- 3. Describing Data Numerically2h 5m
- 4. Probability2h 16m
- 5. Binomial Distribution & Discrete Random Variables3h 6m
- 6. Normal Distribution and Continuous Random Variables2h 11m
- 7. Sampling Distributions & Confidence Intervals: Mean3h 23m
- Sampling Distribution of the Sample Mean and Central Limit Theorem19m
- Distribution of Sample Mean - Excel23m
- Introduction to Confidence Intervals15m
- Confidence Intervals for Population Mean1h 18m
- Determining the Minimum Sample Size Required12m
- Finding Probabilities and T Critical Values - Excel28m
- Confidence Intervals for Population Means - Excel25m
- 8. Sampling Distributions & Confidence Intervals: Proportion1h 12m
- 9. Hypothesis Testing for One Sample3h 29m
- 10. Hypothesis Testing for Two Samples4h 50m
- Two Proportions1h 13m
- Two Proportions Hypothesis Test - Excel28m
- Two Means - Unknown, Unequal Variance1h 3m
- Two Means - Unknown Variances Hypothesis Test - Excel12m
- Two Means - Unknown, Equal Variance15m
- Two Means - Unknown, Equal Variances Hypothesis Test - Excel9m
- Two Means - Known Variance12m
- Two Means - Sigma Known Hypothesis Test - Excel21m
- Two Means - Matched Pairs (Dependent Samples)42m
- Matched Pairs Hypothesis Test - Excel12m
- 11. Correlation1h 6m
- 12. Regression1h 50m
- 13. Chi-Square Tests & Goodness of Fit1h 57m
- 14. ANOVA1h 57m
10. Hypothesis Testing for Two Samples
Two Means - Matched Pairs (Dependent Samples)
Problem 13.3.6
Textbook Question
Using the Wilcoxon Signed-Ranks Test
In Exercises 5–8, refer to the sample data for the given exercises in Section 13-2. Use the Wilcoxon signed-ranks test to test the claim that the matched pairs have differences that come from a population with a median equal to zero. Use a 0.05 significance level.
Exercise 6 “Do Men and Women Talk the Same Amount?”
 Verified step by step guidance
Verified step by step guidance1
Step 1: Understand the Wilcoxon Signed-Ranks Test. This is a nonparametric test used to compare paired data when the assumption of normality is not met. It tests whether the median of the differences between paired observations is equal to zero.
Step 2: Calculate the differences between the paired observations (e.g., the amount of talking by men and women for each pair). For each pair, subtract one value from the other to obtain the differences.
Step 3: Rank the absolute values of the differences, ignoring the signs. Assign ranks starting from 1 for the smallest absolute difference, and handle tied ranks by assigning the average rank to the tied values.
Step 4: Assign the signs of the original differences to the ranks. For example, if a difference was negative, the corresponding rank will be negative; if positive, the rank will remain positive.
Step 5: Compute the test statistic, which is the sum of the positive ranks or the sum of the negative ranks (whichever is smaller). Compare this test statistic to the critical value from the Wilcoxon Signed-Ranks Test table at the 0.05 significance level to determine whether to reject the null hypothesis that the median of the differences is zero.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
6mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Wilcoxon Signed-Ranks Test
The Wilcoxon Signed-Ranks Test is a non-parametric statistical test used to compare two related samples or matched observations. It assesses whether their population mean ranks differ, making it suitable for situations where the data does not meet the assumptions of normality required for parametric tests. This test is particularly useful for analyzing paired data, such as before-and-after measurements.
Recommended video:
Guided course
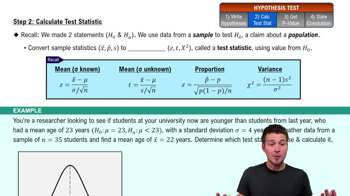
Step 2: Calculate Test Statistic
Significance Level
The significance level, often denoted as alpha (α), is the threshold for determining whether a statistical result is significant. In this context, a significance level of 0.05 indicates that there is a 5% risk of concluding that a difference exists when there is none (Type I error). It helps researchers decide whether to reject the null hypothesis based on the p-value obtained from the test.
Recommended video:
Guided course
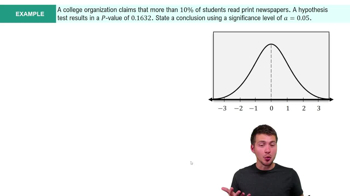
Step 4: State Conclusion Example 4
Median
The median is a measure of central tendency that represents the middle value of a dataset when it is ordered from least to greatest. Unlike the mean, the median is less affected by outliers and skewed data, making it a robust measure for understanding the central location of a distribution. In the context of the Wilcoxon Signed-Ranks Test, the claim being tested is whether the differences between matched pairs have a median of zero.
Recommended video:
Guided course

Calculating the Median

 8:33m
8:33mWatch next
Master Introduction to Matched Pairs with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice
Multiple Choice
