Table of contents

1. Intro to Stats and Collecting Data1h 14m
2. Describing Data with Tables and Graphs1h 55m
3. Describing Data Numerically2h 5m
4. Probability2h 16m
5. Binomial Distribution & Discrete Random Variables3h 6m
6. Normal Distribution and Continuous Random Variables2h 11m
7. Sampling Distributions & Confidence Intervals: Mean3h 23m
8. Sampling Distributions & Confidence Intervals: Proportion1h 12m
- Sampling Distribution of Sample Proportion
  29m
- Confidence Intervals for Population Proportion
  42m
9. Hypothesis Testing for One Sample3h 29m
10. Hypothesis Testing for Two Samples4h 50m
11. Correlation1h 6m
12. Regression1h 50m
13. Chi-Square Tests & Goodness of Fit1h 57m
14. ANOVA1h 57m

12. Regression

Residuals

Statistics

12. Regression

Residuals

Previous problemNext problem

Struggling with Statistics?

Join thousands of students who trust us to help them ace their exams!Watch the first video

Multiple Choice

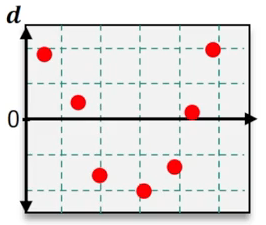
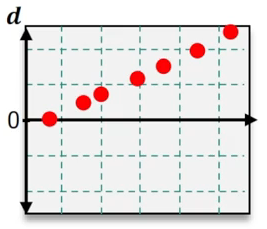
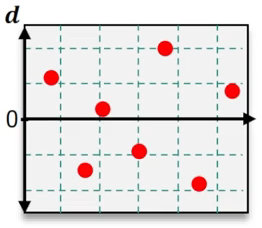
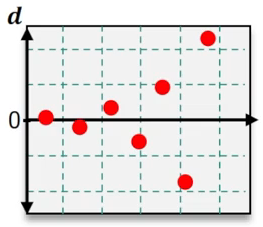
Which of the following residual plots suggest that a linear regression model is appropriate?

Scatter plot with red dots representing residuals, indicating potential appropriateness of a linear regression model.

Red dots on a grid represent a residual plot, indicating a potential linear relationship in the data.

A grid plot showing red dots representing residuals, indicating potential linear regression model appropriateness.

Residual plot with red dots representing data points, indicating the appropriateness of a linear regression model.

Previous problemNext problem

Verified step by step guidance

Step 1: Understand the purpose of residual plots. Residual plots are used to assess the appropriateness of a linear regression model. A good residual plot for linear regression should show no discernible pattern, with residuals randomly scattered around zero.

Step 2: Analyze the first residual plot. Check if the residuals are randomly scattered around the horizontal axis (zero line) without forming any systematic pattern.

Step 3: Analyze the second residual plot. Look for any trends or systematic patterns, such as a curve or increasing/decreasing residuals, which would indicate that a linear model is not appropriate.

Step 4: Analyze the third residual plot. Again, check for randomness in the distribution of residuals around the zero line. If the residuals are evenly scattered, this suggests a linear model may be appropriate.

Step 5: Analyze the fourth residual plot. Look for any systematic patterns, such as clusters or trends, which would suggest that a linear model is not suitable. Random scatter indicates appropriateness for linear regression.