Table of contents

1. Intro to Stats and Collecting Data55m
2. Describing Data with Tables and Graphs1h 55m
3. Describing Data Numerically1h 45m
4. Probability2h 16m
5. Binomial Distribution & Discrete Random Variables2h 33m
6. Normal Distribution and Continuous Random Variables1h 38m
7. Sampling Distributions & Confidence Intervals: Mean1h 53m
8. Sampling Distributions & Confidence Intervals: Proportion1h 12m
- Sampling Distribution of Sample Proportion
  29m
- Confidence Intervals for Population Proportion
  42m
9. Hypothesis Testing for One Sample2h 19m
10. Hypothesis Testing for Two Samples3h 22m
11. Correlation1h 6m
12. Regression1h 4m
13. Chi-Square Tests & Goodness of Fit1h 20m
14. ANOVA1h 0m

4. Probability

Basic Concepts of Probability

Statistics

4. Probability

Basic Concepts of Probability

Previous problemNext problem

1:24 minutes

Problem 5.1.19a

Textbook Question

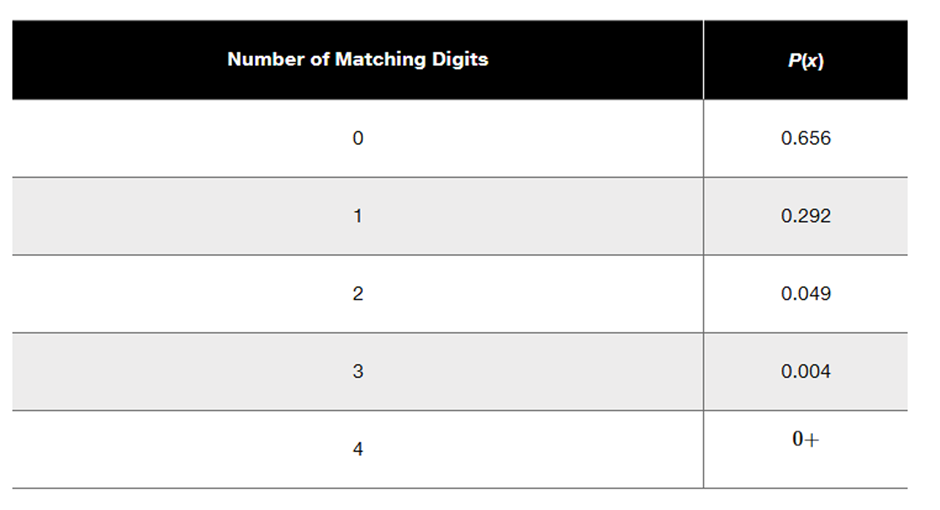
Lottery. In Exercises 15–20, refer to the accompanying table, which describes probabilities for the California Daily 4 lottery. The player selects four digits with repetition allowed, and the random variable x is the number of digits that match those in the same order that they are drawn (for a “straight” bet).

Using Probabilities for Significant Events

a. Find the probability of getting exactly 3 matches.

Verified step by step guidance

Step 1: Understand the problem. The goal is to find the probability of getting exactly 3 matches in the California Daily 4 lottery. The table provided lists the probabilities for different numbers of matching digits (x).

Step 2: Locate the relevant probability in the table. The table shows the probability P(x) for each number of matching digits. For x = 3 (exactly 3 matches), the corresponding probability is 0.004.

Step 3: Interpret the probability. The value 0.004 represents the likelihood of selecting 3 digits that match the drawn digits in the same order during a 'straight' bet.

Step 4: Verify the context. Ensure that the table and problem description align with the calculation. The table explicitly provides the probability for x = 3, so no further computation is needed.

Step 5: Conclude the process. The probability of getting exactly 3 matches is directly obtained from the table as 0.004. This concludes the solution process.

Verified video answer for a similar problem:

This video solution was recommended by our tutors as helpful for the problem above

Video duration:

Play a video:

Was this helpful?

Key Concepts

Here are the essential concepts you must grasp in order to answer the question correctly.

Probability Distribution

A probability distribution describes how the probabilities of a random variable are distributed across its possible values. In this case, the random variable x represents the number of matching digits in the lottery, and the table provides the probabilities for each possible outcome (0 to 4 matches). Understanding this distribution is crucial for calculating the likelihood of specific events, such as getting exactly 3 matches.

Random Variable

A random variable is a numerical outcome of a random phenomenon. In the context of the lottery question, the random variable x indicates the number of digits that match the drawn numbers in the same order. Recognizing how random variables function helps in analyzing the probabilities associated with different outcomes in probabilistic scenarios.

Calculating Probabilities

Calculating probabilities involves determining the likelihood of a specific event occurring based on a probability distribution. For this question, to find the probability of getting exactly 3 matches, one would refer to the provided table and identify the corresponding probability value, which is 0.004. This process is fundamental in statistics for making informed predictions about random events.

Watch next

Master Introduction to Probability with a bite sized video explanation from Patrick

Start learning

Related Videos

Related Practice

Textbook Question

Notation For a polygraph (lie detector) used when a subject is presented with a question, let L= the subject lied and let Y = the polygraph indicated that the subject told a lie. Use your own words to translate the notation P (Y|L) into a verbal statement.

Textbook Question

Significant For 100 births, P(exactly 56 girls) and P(56 or more girls) Is 56 girls in 100 births a significantly high number of girls? Which probability is relevant to answering that question?

Textbook Question

Lottery. In Exercises 15–20, refer to the accompanying table, which describes probabilities for the California Daily 4 lottery. The player selects four digits with repetition allowed, and the random variable x is the number of digits that match those in the same order that they are drawn (for a “straight” bet).

Using Probabilities for Significant Events

a. Find the probability of getting exactly 2 matches.

Textbook Question

Using Probabilities for Significant Events

b. Find the probability of getting 2 or more matches.

Textbook Question

Using Probabilities for Significant Events

c. Which probability is relevant for determining whether 3 is a significantly high number of matches: the result from part (a) or part (b)?

Textbook Question

Using Probabilities for Significant Events

a. Find the probability of getting exactly 1 match.

Textbook Question