Here are the essential concepts you must grasp in order to answer the question correctly.
Sample Mean
The sample mean is the average of a set of values, calculated by summing all the values and dividing by the number of observations. In this context, it represents the average salary of employees after a uniform pay cut. The mean is sensitive to changes in data, so a consistent adjustment, like a pay cut, will directly affect its value.
Recommended video:
Sampling Distribution of Sample Proportion
Sample Standard Deviation
The sample standard deviation measures the amount of variation or dispersion in a set of values. It indicates how much individual salaries deviate from the sample mean. When all salaries are uniformly adjusted (e.g., a pay cut), the standard deviation remains unchanged, as the relative differences between salaries do not alter.
Recommended video:
Calculating Standard Deviation
Uniform Transformation
A uniform transformation refers to applying the same change to all data points in a dataset. In this case, reducing each salary by $2000 is a uniform transformation. This type of adjustment affects the mean but not the standard deviation, as it does not alter the distribution of the data, only shifts it.
Recommended video:
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem: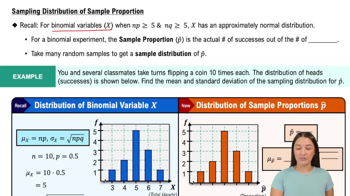


 8:45m
8:45m