Building Basic Skills and Vocabulary
Describe the relationship between quartiles and percentiles.
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem: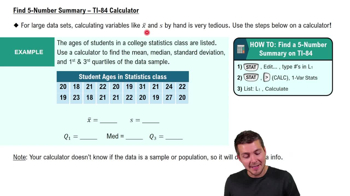
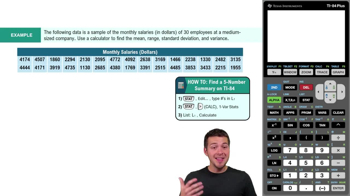


 4:51m
4:51mMaster Find 5-Number Summary - TI-84 Calculator with a bite sized video explanation from Patrick
Start learning