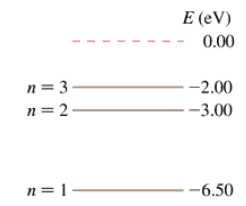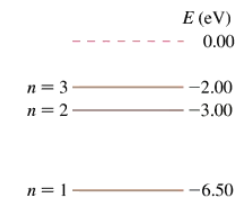An electron confined in a one-dimensional box emits a 200 nm photon in a quantum jump from n = 2 to n = 1. What is the length of the box?

The first three energy levels of the fictitious element X are shown in FIGURE P38.54. What is the ionization energy of element X?

The first three energy levels of the fictitious element X are shown in FIGURE P38.54. What wavelengths are observed in the absorption spectrum of element X? Express your answers in nm.

The absorption spectrum of an atom consists of the wavelengths 200 nm, 300 nm, and 500 nm. b. What wavelengths are seen in the atom’s emission spectrum?

The first three energy levels of the fictitious element X were shown in Figure P38.54. An electron with a speed of 1.4×10⁶ m/s collides with an atom of element X. Shortly afterward, the atom emits a photon with a wavelength of 1240 nm. What was the electron’s speed after the collision? Assume that, because the atom is much more massive than the electron, the recoil of the atom is negligible. Hint: The energy of the photon is not the energy transferred to the atom in the collision.

What wavelength photon does a hydrogen atom emit in a 200→199 transition?

What is the difference in the wavelengths emitted in a 199→2 transition and a 200→2 transition?

Consider a hydrogen atom in stationary state n. On average, an atom stays in the n = 2 state for 1.6 ns before undergoing a transition to the n = 1 state. On average, how many revolutions does the electron make before the transition?

Draw an energy-level diagram, similar to Figure 38.21, for the He+ ion. On your diagram: Show the first five energy levels. Label each with the values of n and E_n.

Draw an energy-level diagram, similar to Figure 38.21, for the He+ ion. On your diagram: Show the ionization limit.

Draw an energy-level diagram, similar to Figure 38.21, for the He+ ion. On your diagram: Show all possible emission transitions from the n = 4 energy level.

Very large, hot stars—much hotter than our sun—can be identified by the way in which He⁺ ions in their atmosphere absorb light. What are the three longest wavelengths, in nm, in the Balmer series of He⁺?

INT Two hydrogen atoms collide head-on. The collision brings both atoms to a halt. Immediately after the collision, both atoms emit a 121.6 nm photon. What was the speed of each atom just before the collision?

INT A beam of electrons is incident upon a gas of hydrogen atoms. What minimum speed must the electrons have to cause the emission of 656 nm light from the 3→2 transition of hydrogen?

INT A beam of electrons is incident upon a gas of hydrogen atoms. Through what potential difference must the electrons be accelerated to have this speed?

The electrons in a cathode-ray tube are accelerated through a 250 V potential difference and then shot through a 33-nm-diameter circular aperture. What is the diameter of the bright spot on an electron detector 1.5 m behind the aperture?

Consider an electron undergoing cyclotron motion in a magnetic field. According to Bohr, the electron’s angular momentum must be quantized in units of ℏ. Compute the first four allowed radii in a 1.0 T magnetic field.

Consider an electron undergoing cyclotron motion in a magnetic field. According to Bohr, the electron’s angular momentum must be quantized in units of ℏ. Find an expression for the allowed energy levels E_n in terms of ℏ and the cyclotron frequency f_cyc.