Back
BackProblem 2b
Figure 37.7 identified the wavelengths of four lines in the Balmer series of hydrogen. Predict the wavelength of the fifth line in the spectrum.
Problem 6
A 2.0-cm-diameter metal sphere is glowing red, but a spectrum shows that its emission spectrum peaks at an infrared wavelength of 2.0 μm. How much power does the sphere radiate? Assume e=1 .
Problem 7
A ceramic cube 3.0 cm on each side radiates heat at 630 W. At what wavelength, in μm, does its emission spectrum peak? Assume e=1.
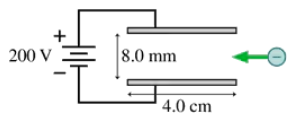
Problem 9
Electrons pass through the parallel electrodes shown in FIGURE EX37.9 with a speed of 5.0×106 m/s. What magnetic field strength and direction will allow the electrons to pass through without being deflected? Assume that the magnetic field is confined to the region between the electrodes.
Problem 10a
An electron in a cathode-ray beam passes between 2.5-cm-long parallel-plate electrodes that are 5.0 mm apart. A 2.0 mT, 2.5-cm-wide magnetic field is perpendicular to the electric field between the plates. The electron passes through the electrodes without being deflected if the potential difference between the plates is 600 V. What is the electron's speed?
Problem 10b
An electron in a cathode-ray beam passes between 2.5-cm-long parallel-plate electrodes that are 5.0 mm apart. A 2.0 mT, 2.5-cm-wide magnetic field is perpendicular to the electric field between the plates. The electron passes through the electrodes without being deflected if the potential difference between the plates is 600 V. If the potential difference between the plates is set to zero, what is the electron's radius of curvature in the magnetic field?
Problem 11c
A 0.80-μm-diameter oil droplet is observed between two parallel electrodes spaced 11 mm apart. The droplet hangs motionless if the upper electrode is 20 V more positive than the lower electrode. The density of the oil is 885 kg/m3. Does the droplet have a surplus or a deficit of electrons? How many?
Problem 14b
Determine the speed of a 15 MeV helium atom.
Problem 16a
Express in eV (or keV or MeV if more appropriate): The kinetic energy of an electron moving with a speed of 5.0 x 10⁶ m/s .
Problem 18
A parallel-plate capacitor with a 1.0 mm plate separation is charged to 75 V. With what kinetic energy, in eV, must a proton be launched from the negative plate if it is just barely able to reach the positive plate?
Problem 19
How many electrons, protons, and neutrons are contained in the following atoms or ions: (a) ¹⁰B, (b) ¹³N⁺, and (c) ¹⁷O⁺⁺⁺?
Problem 20
Identify the isotope that is 11 times as heavy as ¹²C and has 18 times as many protons as ⁶Li . Give your answer in the form ᴬS, where S is the symbol for the element. See Appendix C: Atomic and Nuclear Data.
Problem 23b
Consider the gold isotope 197Au. The gold nucleus has a diameter of 14.0 fm. What is the density of matter in a gold nucleus?
Problem 27b
What is the velocity, as a fraction of c, of an electron with 2.0 GeV total energy? Hint: This problem uses relativity.
Problem 31
The factor γ appears in many relativistic expressions. A value γ = 1.01 implies that relativity changes the Newtonian values by approximately 1% and that relativistic effects can no longer be ignored. At what kinetic energy, in MeV, is γ = 1.01 for (a) an electron, (b) a proton, and (c) an alpha particle?
Problem 32
The fission process n + ²³⁵U → ²³⁶U → ¹⁴⁴Ba + ⁸⁹Kr + 3n converts 0.185 u of mass into the kinetic energy of the fission products. What is the total kinetic energy in MeV?
Problem 36
In one of Thomson’s experiments he placed a thin metal foil in the electron beam and measured its temperature rise. Consider a cathode-ray tube in which electrons are accelerated through a 2000 V potential difference, then strike a 10 mg copper foil. What is the electron-beam current if the foil temperature rises 6.0°C in 10 s? Assume no loss of energy by radiation or other means. The specific heat of copper is 385 J/kg K .
Problem 41
A ²²²Rn atom (radon) in a 0.75 T magnetic field undergoes radioactive decay, emitting an alpha particle in a direction perpendicular to . The alpha particle begins cyclotron motion with a radius of 45 cm. With what energy, in MeV, was the alpha particle emitted?
Problem 44a
The oxygen nucleus ¹⁶O has a radius of 3.0 fm. With what speed must a proton be fired toward an oxygen nucleus to have a turning point 1.0 fm from the surface? Assume the nucleus remains at rest.
Problem 45b
To initiate a nuclear reaction, an experimental nuclear physicist wants to shoot a proton into a 5.50-fm-diameter ¹²C nucleus. The proton must impact the nucleus with a kinetic energy of 3.00 MeV. Assume the nucleus remains at rest. Through what potential difference must the proton be accelerated from rest to acquire this speed?
Problem 46b
A classical atom that has an electron orbiting at frequency ⨍ would emit electromagnetic waves of frequency ⨍ because the electron's orbit, seen edge-on, looks like an oscillating electric dipole. What is the total mechanical energy of this atom?
Problem 48a
Physicists first attempted to understand the hydrogen atom by applying the laws of classical physics. Consider an electron of mass m and charge −e in a circular orbit of radius r around a proton of charge +e. Use Newtonian physics to show that the total energy of the atom is E =−e²/8πϵ₀𝓇
Problem 48c
Physicists first attempted to understand the hydrogen atom by applying the laws of classical physics. Consider an electron of mass m and charge −e in a circular orbit of radius r around a proton of charge +e. The minimum energy needed to ionize a hydrogen atom (i.e., to remove the electron) is found experimentally to be 13.6 eV. From this information, what are the electron's speed and the radius of its orbit?
Problem 49a
Consider an oil droplet of mass m and charge q. We want to determine the charge on the droplet in a Millikan-type experiment. We will do this in several steps. Assume, for simplicity, that the charge is positive and that the electric field between the plates points upward. An electric field is established by applying a potential difference to the plates. It is found that a field of strength E₀ will cause the droplet to be suspended motionless. Write an expression for the droplet's charge in terms of the suspending field E₀ and the droplet's weight mg.
Problem 49c
Consider an oil droplet of mass m and charge q. We want to determine the charge on the droplet in a Millikan-type experiment. We will do this in several steps. Assume, for simplicity, that the charge is positive and that the electric field between the plates points upward. A spherical object of radius r moving slowly through the air is known to experience a retarding force Fdrag = −6πηr v where η is the viscosity of the air. Use this and your answer to part b to show that a spherical droplet of density ρ falling with a terminal velocity vterm has a radius.