Back
BackProblem 1
An experiment has four possible outcomes, labeled A to D. The probability of A is PA = 40% and of B is PB = 30%. Outcome C is twice as probable as outcome D. What are the probabilities PC and PD?
Problem 8
In one experiment, 2000 photons are detected in a 0.10-mm-wide strip where the amplitude of the electromagnetic wave is 10 V/m. How many photons are detected in a nearby 0.10-mm-wide strip where the amplitude is 30 V/m?
Problem 9
When 5×1012 photons pass through an experimental apparatus, 2.0×109 land in a 0.10-mm-wide strip. What is the probability density at this point?
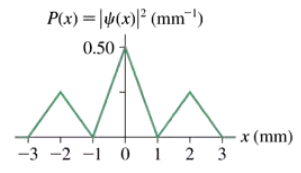
Problem 12b
FIGURE EX39.12 shows the probability density for an electron that has passed through an experimental apparatus. If 1.0×106 electrons are used, what is the expected number that will land in a 0.010-mm-wide strip at 2.000 mm?
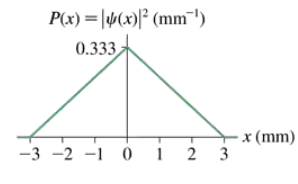
Problem 13a
FIGURE EX39.13 shows the probability density for an electron that has passed through an experimental apparatus. What is the probability that the electron will land in a 0.010-mm-wide strip at x = 0.000 mm?
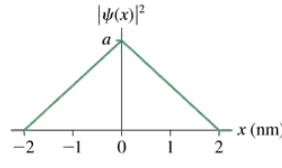
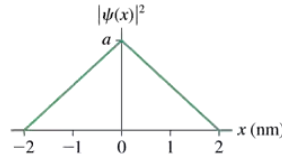
Problem 14a
FIGURE EX39.14 is a graph of |ψ(x)|2 for an electron. What is the value of a?
Problem 14c
FIGURE EX39.14 is a graph of |ψ(x)|2 for an electron. What is the probability that the electron is located between x = 1.0 nm and x = 2.0 nm?
Problem 16b
FIGURE EX39.16 shows the wave function of an electron. Draw a graph of |ψ(x)|2.
Problem 19
A 1.5-μm-wavelength laser pulse is transmitted through a 2.0-GHz-bandwidth optical fiber. How many oscillations are in the shortest-duration laser pulse that can travel through the fiber?
Problem 21
What minimum bandwidth is needed to transmit a pulse that consists of 100 cycles of a 1.0 MHz oscillation?
Problem 25
What is the minimum uncertainty in position, in nm, of an electron whose velocity is known to be between 3×105 m/s and 4 ×105 m/s? Give your answer to one significant figure.
Problem 26a
A 1.0-mm-diameter sphere bounces back and forth between two walls at x = 0 mm and x = 100 mm. The collisions are perfectly elastic, and the sphere repeats this motion over and over with no loss of speed. At a random instant of time, what is the probability that the center of the sphere is at exactly x = 50.0 mm?
Problem 26b
A 1.0-mm-diameter sphere bounces back and forth between two walls at x = 0 mm and x = 100 mm. The collisions are perfectly elastic, and the sphere repeats this motion over and over with no loss of speed. At a random instant of time, what is the probability that the center of the sphere is between x = 49.0 mm and x = 51.0 mm?
Problem 28
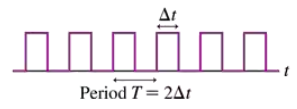
FIGURE P39.28 shows a pulse train. The period of the pulse train is T = 2 Δt, where Δt is the duration of each pulse. What is the maximum pulse-transmission rate (pulses per second) through an electronics system with a 200 kHz bandwidth? (This is the bandwidth allotted to each FM radio station.)
Problem 29b
Consider a single-slit diffraction experiment using electrons. (Single-slit diffraction was described in Section 33.4.) Using Figure 39.5 as a model, draw A graph of |ψ(x)|2 for the electrons on the detection screen.
Problem 30c
An experiment finds electrons to be uniformly distributed over the interval 0 cm ≤ x ≤ 2 cm, with no electrons falling outside this interval. If 106 electrons are detected, how many will be detected in the interval 0.79 to 0.81 cm?
Problem 30d
An experiment finds electrons to be uniformly distributed over the interval 0 cm ≤ x ≤ 2 cm, with no electrons falling outside this interval. What is the probability density at x = 0.80 cm?
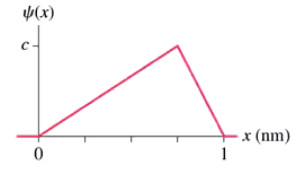
Problem 31a
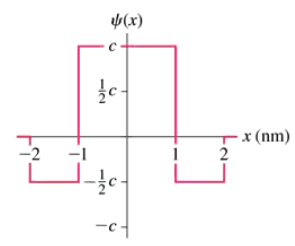
FIGURE P39.31 shows the wave function of a particle confined between x = 0 nm and x = 1.0 nm. The wave function is zero outside this region. Determine the value of the constant c, as defined in the figure.
Problem 31b
FIGURE P39.31 shows the wave function of a particle confined between x = 0 nm and x = 1.0 nm. The wave function is zero outside this region. Draw a graph of the probability density P(x)=|ψ(x)|2
Problem 31d
FIGURE P39.31 shows the wave function of a particle confined between x = 0 nm and x = 1.0 nm. The wave function is zero outside this region. Calculate the probability of finding the particle in the interval 0 nm ≤ x ≤ 0.25 nm.
Problem 36a
Consider the electron wave function where x is in cm. Determine the normalization constant c.
Problem 36b
Consider the electron wave function where x is in cm. Draw a graph of ψ(x) over the interval −2 cm ≤ x ≤ 2 cm. Provide numerical scales on both axes.
Problem 36c
Consider the electron wave function where x is in cm. Draw a graph of |ψ(x)|2 over the interval −2 cm ≤ x ≤ 2 cm. Provide numerical scales.
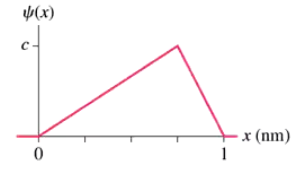
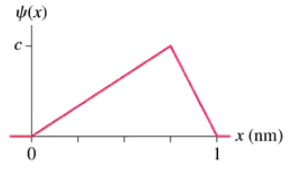
Problem 38a
A particle is described by the wave function where L = 2.0 mm. Sketch graphs of both the wave function and the probability density as functions of x.
Problem 38b
A particle is described by the wave function mm where L = 2.0 mm. Determine the normalization constant c.
Problem 38c
A particle is described by the wave function where L = 2.0 mm. Calculate the probability of finding the particle within 1.0 mm of the origin.
Problem 38d
A particle is described by the wave function where L = 2.0 mm. Interpret your answer to part b by shading the region representing this probability on the appropriate graph in part a.
Problem 39d
Consider the electron wave function where x is in cm. If 104 electrons are detected, how many will be in the interval 0.00 cm ≤ x ≤ 0.50 cm?
Problem 40d
A pulse of light is created by the superposition of many waves that span the frequency range f₀ − (1/2) Δf ≤ f ≤ f₀ + (1/2) Δf, where f₀ = c/λ is called the center frequency of the pulse. Laser technology can generate a pulse of light that has a wavelength of 600 nm and lasts a mere 6.0 fs (1 fs = 1 femtosecond =10−15 s). What is the spatial length of the laser pulse as it travels through space?
Problem 43a
Heavy nuclei often undergo alpha decay in which they emit an alpha particle (i.e., a helium nucleus). Alpha particles are so tightly bound together that it’s reasonable to think of an alpha particle as a single unit within the nucleus from which it is emitted. A 238U nucleus, which decays by alpha emission, is 15 fm in diameter. Model an alpha particle within a 238U nucleus as being in a one-dimensional box. What is the maximum speed an alpha particle is likely to have?