An inductance coil draws 2.2 A dc when connected to a 45-V battery. When connected to a 60.0-Hz 120-V (rms) source, the current drawn is 3.8 A (rms). Determine the inductance and resistance of the coil.

Show that the fraction of electromagnetic energy lost (to thermal energy) per cycle in a lightly damped (R² ≪ 4L/C) LRC circuit is approximately $\frac{\Delta U}{U}=\frac{2\pi R}{L\omega }=\frac{2\pi }{Q}$. The quantity Q can be defined as Q = Lω/R, and is called the Q-value, or quality factor, of the circuit and is a measure of the damping present. A high Q-value means smaller damping and less energy input required to maintain oscillations.

In some experiments, very tiny distances or spaces ( ≈ nm ) can be measured by using capacitance. Consider forming an LC circuit using a parallel-plate capacitor with plate area A, and a known inductance L. If charge is found to oscillate in this circuit at frequency f = ω/2π when the capacitor plates are separated by distance x, show that x = 4π² Aε₀f²L.

In some experiments, very tiny distances or spaces ( ≈ nm ) can be measured by using capacitance. Consider forming an LC circuit using a parallel-plate capacitor with plate area A, and a known inductance L. When the plate separation is changed by ∆x, the circuit’s oscillation frequency will change by ∆f. Show that ∆x/x ≈ 2(∆f/f).

In some experiments, very tiny distances or spaces ( ≈ nm ) can be measured by using capacitance. Consider forming an LC circuit using a parallel-plate capacitor with plate area A, and a known inductance L. If f is on the order of 1 MHz and can be measured to a precision of ∆f = 1 Hz, with what percent accuracy can x be determined? Assume fringing effects at the capacitor’s edges can be neglected.

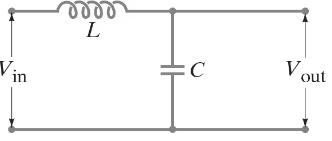
Filter circuit. Figure 30–33 shows a simple filter circuit designed to pass dc voltages with minimal attenuation and to remove, as much as possible, any ac components (such as 60-Hz line voltage that could cause hum in an audio system, for example). Assume V_in = V₁ + V₂ where V₁ is dc and V₂ = V₂₀ sin ωt, and that any resistance is very small. (a) Determine the current through the capacitor: give amplitude and phase (assume R = 0 and X_L > X_C). (b) Show that the ac component of the output voltage, V_2out, equals (Q/C) - V₁ where Q is the charge on the capacitor at any instant, and determine the amplitude and phase of V_2out (c) Show that the attenuation of the ac voltage is greatest when X_C << X_L, and calculate the ratio of the output to input ac voltage in this case. (d) Compare the dc output voltage to input voltage.

Show that if the inductor L in the filter circuit of Fig. 30–33 (Problem 87) is replaced by a large resistor R, there will still be significant attenuation of the ac voltage and little attenuation of the dc voltage if the input dc voltage is high and the current (and power) are low.

Suppose a series LRC circuit has two resistors, R₁ and R₂, two capacitors, C₁ and C₂, and two inductors, L₁ and L₂ all in series. Calculate the total impedance of the circuit.

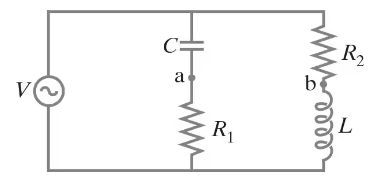
For the circuit shown in Fig. 30–35, show that if the condition R₁ R₂ = L/C is satisfied then the potential difference between points a and b is zero for all frequencies.

In a plasma globe, a hollow glass sphere is filled with low-pressure gas and a small spherical metal electrode is located at its center. Assume an ac voltage source of peak voltage V_o and frequency f is applied between the metal sphere and the ground, and that a person is touching the outer surface of the globe with a fingertip, whose approximate area is 1.0 cm². The equivalent circuit for this situation is shown in Fig. 30–36, where R_G and R_P are the resistances of the gas and the person, respectively, and C is the capacitance formed by the gas, glass, and finger. (a) Determine C assuming it is a parallel-plate capacitor. The conductive gas and the person’s fingertip form the opposing plates of area A = 1.0 cm². The plates are separated by glass (dielectric constant K = 5.0) of thickness d = 2.0 mm. (b) In a typical plasma globe, f = 12 kHz. Determine the reactance X_C of C at this frequency in MΩ. (c) The voltage may be V_o = 2500 V. With this high voltage, the dielectric strength of the gas is exceeded and the gas becomes ionized. In this “plasma” state, the gas emits light (“sparks”) and is highly conductive so that R_G << X_C. Assuming also that R_P << X_C, estimate the peak current that flows in the given circuit. Is this level of current dangerous? (d) If the plasma globe operated at f = 1.0 MHz, estimate the peak current that would flow in the given circuit. Is this level of current dangerous?

<IMAGE>

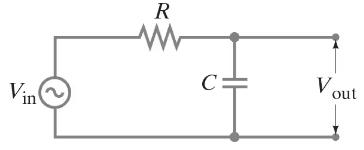
The RC circuit shown in Fig. 30–39 is a low-pass filter because it passes low-frequency ac signals with less attenuation than high-frequency ac signals. (a) Show that the voltage gain is $A=V_{\text{out}}/V_{\text{in}}=1/(4{\pi }^2{f}^2{R}^2{C}^2+1{)}^{\frac{1}{2}}$ (b) Discuss the behavior of the gain A for f → 0 and f → ∞.

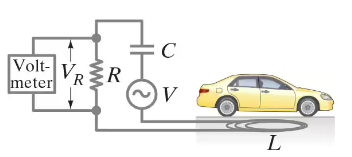
To detect vehicles at traffic lights, wire loops with dimensions on the order of 2 m are often buried horizontally under roadways. Assume the self-inductance of such a coil is L = 5.0 mH and that it is part of an LRC circuit as shown in Fig. 30–40 with C = 0.10 μF and R = 38 Ω. The ac voltage has frequency f and rms voltage V_rms. (a) The frequency f is chosen to match the resonant frequency f₀ of the circuit. Find f₀ and determine what the rms voltage (V_R)_rms across the resistor will be when f = f₀. (b) Assume that f, C, and R never change, but that, when a car is located above the buried coil, the coil’s self-inductance decreases by 10% (due to induced eddy currents in the car’s metal parts). Determine by what factor the voltage (V_R)_rms decreases in the presence of a car in comparison to no car above the loop and thus how it detects the presence of a car. (c) Describe how the eddy currents induced in the car reduce L. [Hint: Recall Eq. 30–4, the definition of inductance.]