Suppose an air-gap capacitor has circular plates of radius r = 2.5 cm and separation d = 1.6 mm. A 68.0-Hz emf, ε = ε₀ cos ωt, is applied to the capacitor. The maximum displacement current is 35 μA. Determine the maximum conduction current I. Neglect fringing.

Suppose an air-gap capacitor has circular plates of radius r = 2.5 cm and separation d = 1.6 mm. A 68.0-Hz emf, ε = ε₀ cos ωt, is applied to the capacitor. The maximum displacement current is 35 μA. Determine the value of ε₀. Neglect fringing.

Suppose an air-gap capacitor has circular plates of radius r = 2.5 cm and separation d = 1.6 mm. A 68.0-Hz emf, ε = ε₀ cos ωt, is applied to the capacitor. The maximum displacement current is 35 μA. Determine the maximum value of dΦE/dt between the plates. Neglect fringing.

Suppose that a circular parallel-plate capacitor has radius r₀ = 3.0 cm and plate separation d = 5.0 mm. A sinusoidal potential difference V = V₀ sin (2𝝅ft) is applied across the plates, where V₀ = 180 V and f = 60 Hz. In the region between the plates, show that the magnitude of the induced magnetic field is given by B = B₀(r) cos (2𝝅ft), where B₀(r) is a function of the radial distance r from the capacitor’s central axis.

Suppose that a circular parallel-plate capacitor has radius r₀ = 3.0 cm and plate separation d = 5.0 mm. A sinusoidal potential difference V = V₀ sin (2𝝅ft) is applied across the plates, where V₀ = 180 V and f = 60 Hz. Determine the expression for the amplitude B₀(r) of this time-dependent (sinusoidal) field when r ≤ r₀ and when r > r₀.

In an EM wave traveling west, the B field oscillates up and down vertically and has a frequency of 85.0 kHz and an rms strength of 7.75 x 10⁻⁹ T. Determine the frequency and rms strength of the electric field. What is the direction of the electric field oscillations?

(a) When a circular parallel-plate capacitor is being charged as in Example 31–1, show that the Poynting vector $\overrightarrow{S}$ points radially inward toward the center of the capacitor, parallel to the plates.

(b) Integrate $\overrightarrow{S}$ over the cylindrical boundary of the capacitor gap to show that the rate at which energy enters the capacitor is equal to the rate at which electrostatic energy is being stored in the electric field of the capacitor (Section 24–4). Ignore fringing of $\overrightarrow{E}$.

(III) (a) When a circular parallel-plate capacitor is being charged as in Example 31–1, show that the Poynting vector $\overrightarrow{S}$ points radially inward toward the center of the capacitor, parallel to the plates.

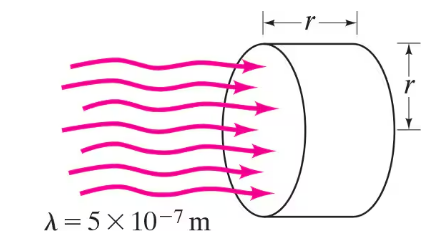
(II) Laser light can be focused (at best) to a spot with a radius r equal to its wavelength ⋋. Suppose a 1.0-W beam of green laser light (⋋ = 5 x 10^-7 m) forms such a spot and illuminates a cylindrical object of radius r and length r (Fig. 31–25). Estimate (a) the radiation pressure and force on the object, and (b) its acceleration, if its density equals that of water and it absorbs all the radiation. [This order-of-magnitude calculation convinced researchers of the feasibility of “optical tweezers,” page 916.]

Suppose you have a car with a 100-hp engine. How large a solar panel would you need to replace the engine with solar power? Assume that the solar panels can utilize 20% of the maximum solar energy that reaches the Earth’s surface (1000 W/m²). Explain why or why not this is practical.

Compare 1030 on the AM dial to 103.1 on FM. Which has the longer wavelength, and by what factor is it larger?

An amateur radio operator wishes to build a receiver that can tune a range from 14.0 MHz to 15.0 MHz. A variable capacitor has a minimum capacitance of 95 pF.

(a) What is the required value of the inductance?

(b) What is the maximum capacitance used on the variable capacitor?

A satellite beams microwave radiation with a power of 16 kW toward the Earth’s surface, 550 km away. When the beam strikes Earth, its circular diameter is about 1500 m. Find the rms electric field strength of the beam.

Who will hear the voice of a singer first: a person in the balcony 50.0 km away from the stage (see Fig. 31–26), or a person 1800 km away at home whose ear is next to the radio listening to a live broadcast? Roughly how much sooner? Assume the microphone is a few centimeters from the singer and the temperature is 20℃.

<IMAGE>

A global positioning system (GPS) functions by determining the travel times for EM waves from various satellites to a moving GPS receiver on Earth (car or hiker). If the receiver is to detect a change in the receiver’s position on the order of 3 m, what is the associated change in travel time (in ns) that must be measured?

Radio-controlled clocks throughout the United States receive a radio signal from a transmitter in Fort Collins, Colorado, that accurately (within a microsecond) marks the beginning of each minute. A slight amount of time is added by a clock at any location to correct for the signal travel time to the clock from Fort Collins. Assuming Fort Collins is no more than 3000 km from any point in the U.S., what is the longest travel-time delay?

The average intensity of a particular TV station’s signal is 1.0 x 10^-13 W/m² when it arrives at a 33-cm-diameter satellite TV antenna. (a) Calculate the total energy received by the antenna during 3.0 hours of viewing this station’s programs. (b) Estimate the amplitudes of the E and B fields of the EM wave.

What length of antenna would be appropriate for a portable device that could receive satellite TV?

A powerful laser portrayed in a movie provides a 3-mm-diameter beam of green light with a power of 3 W. A good agent inside a spacecraft aims the laser beam at an enemy astronaut hovering outside. The mass of the enemy astronaut is 120 kg and the spacecraft 185,000 kg. (a) Determine the “radiation-pressure” force exerted on the enemy by the laser beam assuming her suit is perfectly reflecting. (b) If the enemy is 30 m from the spacecraft’s center of mass, estimate the gravitational force the spacecraft exerts on the enemy. (c) Which of the two forces is larger, and by what factor?

Show that displacement current, ε₀ (dΦE/dt), has the SI units of amperes.

What is the maximum power level of a radio station so as to avoid electrical breakdown of air at a distance of 0.75 m from the transmitting antenna? Assume the antenna is a point source. Air breaks down in an electric field of about 3 x 10⁶ V/m.

Imagine that a steady current I flows in a straight cylindrical wire of radius R₀ and resistivity ρ.

(a) If the current is then changed at a rate dI/dt, show that a displacement current ID exists in the wire of magnitude ε₀ρ(dI/dt).

(b) If the current in a copper wire is changed at the rate of 1.0 A/ms, determine the magnitude of ID.

(c) Determine the magnitude of the magnetic field BD created by ID at the surface of a copper wire with R₀ = 1.00 mm. Compare (as a ratio) BD with the field created at the surface of the wire by a steady current of 1.0 A.

Suppose a 25-kW radio station emits EM waves uniformly in all directions. What is the rms voltage induced in a 1.0-m-long vertical car antenna (c) 1.0 km away, (d) 50 km away?

How large an emf (rms) will be generated in an antenna that consists of a circular coil 2.2 cm in diameter having 280 turns of wire, when an EM wave of frequency 810 kHz transporting energy at an average rate of 1.0 x 10⁻⁴ W/m² passes through it? [Hint: You can use Eq. 29–4 (for a generator) because that equation can be applied to an observer moving with the generator’s coil as it rotates at ω = 2𝝅f with f the frequency of the magnetic field.]

Suppose that a right-moving EM wave overlaps with a left-moving EM wave so that, in a certain region of space, the total electric field in the y direction and magnetic field in the z direction are given by Eᵧ = E₀ sin(kx - ωt) + E₀ sin(kx + ωt) and Bz = B₀ sin(kx - ωt) - B₀ sin(kx + ωt). Determine the Poynting vector and find the x locations at which it is zero at all times.