Back
BackProblem 1
The magnetic flux through a coil of wire containing two loops changes at a constant rate from -68 Wb to +48 Wb in 0.42 s. What is the emf induced in the coil?
Problem 9
A circular loop in the plane of the paper lies in a 0.65-T uniform magnetic field pointing into the paper. The loop’s diameter changes from 20.0 cm to 8.0 cm in 0.50 s. What is (a) the direction of the induced current, (b) the magnitude of the average induced emf, and (c) the average induced current if the coil resistance is 2.5Ω?
Problem 29
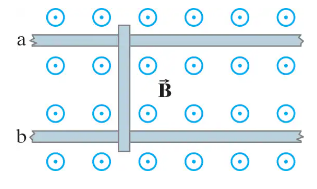
(II) A conducting rod rests on two long frictionless parallel rails in a magnetic field (⊥ to the rails and rod) as in Fig. 29–53. (a) If the rails are horizontal and the rod is given an initial push, will the rod travel at constant speed even though a magnetic field is present? (b) Suppose at t = 0, when the rod has speed v = v0, the two rails are connected electrically by a wire from point a to point b. Assuming the rod has resistance R and the rails have negligible resistance, determine the speed of the rod as a function of time. Discuss your answer.
Problem 30
(III) Suppose a conducting rod (mass m, resistance R) rests on two frictionless and resistanceless parallel rails a distance ℓ apart in a uniform magnetic field (⊥ to the rails and to the rod) as in Fig. 29–53. At t = 0, the rod is at rest and a source of emf is connected to the points a and b. Determine the speed of the rod as a function of time if (a) the source puts out a constant current I, (b) the source puts out a constant emf ε₀. (c) Does the rod reach a terminal speed in either case? If so, what is it?
Problem 44
A transformer is designed to change 117 V into 13,500 V, and there are 172 turns in the primary coil. How many turns are in the secondary coil?
Problem 46
A transformer has 680 turns in the primary coil and 85 in the secondary coil. What kind of transformer is this, and by what factor does it change the voltage? By what factor does it change the current?
Problem 47
Neon signs require 12 kV for their operation. To operate from a 240-V line, what must be the ratio of secondary to primary turns of the transformer? What would the voltage output be if the transformer were connected in reverse?
Problem 48
A model-train transformer plugs into 120-V ac and draws 0.35 A while supplying 6.5 A to the train.
(a) What voltage is present across the tracks?
(b) Is the transformer step-up or step-down?
Problem 49
If 75 MW of power at 45 kV (rms) arrives at a town from a generator via transmission lines of total resistance 3.0 Ω, calculate (a) the emf at the generator end of the lines, and (b) the fraction of the power generated that is wasted in the lines.
Problem 52
(II) For the electric power transmission system shown in Fig. 29–26, what is the ratio Ns/Np for (a) the step-up transformer, (b) the step-down transformer next to the home?
Problem 55
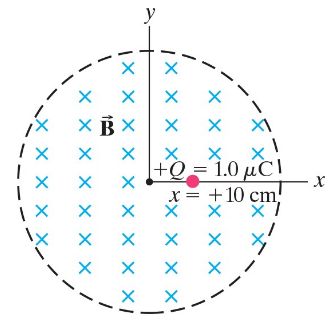
(III) In a circular region, there is a uniform magnetic field pointing into the page (Fig. 29–56). An xy coordinate system has its origin at the circular region’s center. A free positive point charge +Q = 1.0 μC is initially at rest at a position x = +10 cm on the x axis. If the magnitude of the magnetic field is now decreased at a rate of -0.10 T/s, what force (magnitude and direction) will act on +Q?
Problem 61
A circular loop of area 12 m² encloses a magnetic field perpendicular to the plane of the loop; its magnitude is B(t) = (8.0 T/s)t. The loop is connected to a 7.5-Ω resistor and a 6.5-pF capacitor in series. When fully charged, how much charge is stored on the capacitor?
Problem 62
The primary windings of a transformer which has an 85% efficiency are connected to 110-V ac. The secondary windings are connected across a 2.4-Ω, 75-W lightbulb.
(a) Calculate the current through the primary windings of the transformer.
(b) Calculate the ratio of the number of primary windings of the transformer to the number of secondary windings of the transformer.
Problem 65ab
A high-intensity desk lamp is rated at 35 W but requires only 12 V. It contains a transformer that converts 120-V household voltage.
(a) Is the transformer step-up or step-down?
(b) What is the current in the secondary coil when the lamp is on?
Problem 65cd
A high-intensity desk lamp is rated at 35 W but requires only 12 V. It contains a transformer that converts 120-V household voltage.
(c) What is the current in the primary coil?
(d) What is the resistance of the bulb when on?
Problem 67
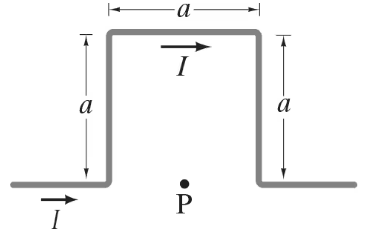
Determine the magnetic field at a point P due to a very long wire with a square bend as shown in Fig. 28–63. The point P is halfway between the two corners.
Problem 75
What is the energy dissipated as a function of time in a circular loop of 18 turns of wire having a radius of 10.0 cm and a resistance of 2.0 Ω if the plane of the loop is perpendicular to a magnetic field given by B(t) = B₀e⁻ᵗ/ʳ with B₀ = 0.50 T and τ = 0.10 s?
Problem 78
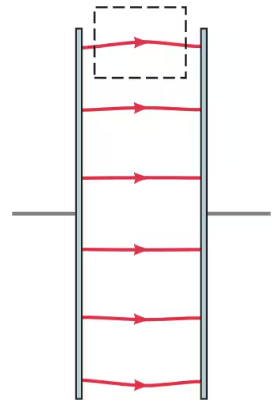
Apply Faraday’s law, in the form of Eq. 29–8, to show that the static electric field between the plates of a parallel-plate capacitor cannot drop abruptly to zero at the edges, but must, in fact, fringe. Use the path shown dashed in Fig. 29–61. [Hint: Assume the contrary: that there is no fringing. Show that this assumption leads to a contradiction.]
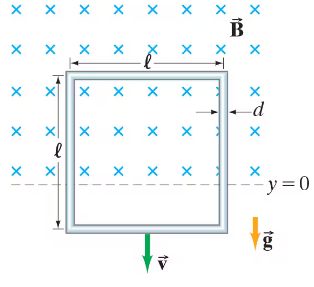
Problem 82
In a certain region of space near Earth’s surface, a uniform horizontal magnetic field of magnitude B exists above a level defined to be y = 0. Below y = 0, the field abruptly becomes zero (Fig. 29–63). A vertical square wire loop has resistivity ρ, mass density ρm, diameter d, and side length ℓ. It is initially at rest with its lower horizontal side at y = 0 and is then allowed to fall under gravity, with its plane perpendicular to the direction of the magnetic field. (a) While the loop is still partially immersed in the magnetic field (as it falls into the zero-field region), determine the magnetic “drag” force that acts on it at the moment when its speed is υ. (b) Assume that the loop achieves a constant terminal velocity VT before its upper horizontal side exits the field. Determine a formula for VT. (c) If the loop is made of copper and B = 0.80 T, find VT.
Problem 85a
In an experiment, a coil was mounted on a low-friction cart that moved through the magnetic field B of a permanent magnet. The speed of the cart v and the induced voltage V were simultaneously measured, as the cart moved through the magnetic field, using a computer-interfaced motion sensor and a voltmeter. The Table below shows the collected data:
Make a graph of the induced voltage, V, vs. the speed, v. Determine a best-fit linear equation for the data. Theoretically, the relationship between V and v is given by V = BN𝓁𝓋 where N is the number of turns of the coil, B is the magnetic field, and ℓ is the average of the inside and outside widths of the coil. In the experiment, B = 0.126 T, N = 50, and ℓ = 0.0561 m.
Problem 85b
In an experiment, a coil was mounted on a low-friction cart that moved through the magnetic field B of a permanent magnet. The speed of the cart v and the induced voltage V were simultaneously measured, as the cart moved through the magnetic field, using a computer-interfaced motion sensor and a voltmeter. The Table below shows the collected data:
Find the % error between the slope of the experimental graph and the theoretical value for the slope.