The 1100-kg mass of a car includes four tires, each of mass 35 kg (including wheels) and diameter 0.80 m. Assume each tire and wheel combination acts as a solid cylinder. Determine the fraction of the kinetic energy in the tires and wheels.

On a 12.0-cm-diameter audio compact disc (CD), digital bits of information are encoded sequentially along an outward spiraling path. The spiral starts at radius R₁ = 2.5 cm and winds its way out to radius R₂ = 5.8 cm. To read the digital information, a CD player rotates the CD so that the player’s readout laser scans along the spiral’s sequence of bits at a constant linear speed of 1.25 m/s. Thus the player must accurately adjust the rotational frequency ƒ of the CD as the laser moves outward. Determine the values for ƒ (in units of rpm) when the laser is located at R₁ and when it is at R₂.

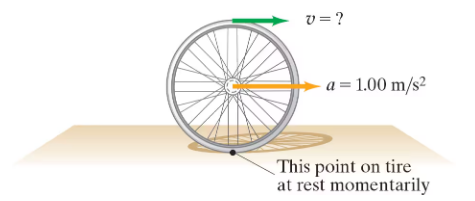
A cyclist accelerates from rest at a rate of 1.00 m/s². How fast will a point at the top of the rim of the tire (diameter = 68.0 cm) be moving after 2.75 s? [Hint: At any moment, the lowest point on the tire is in contact with the ground and is at rest—see Fig. 10–69.]

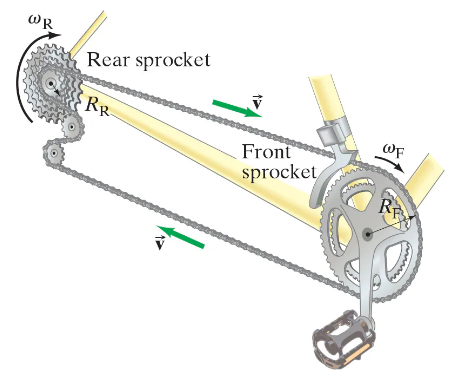
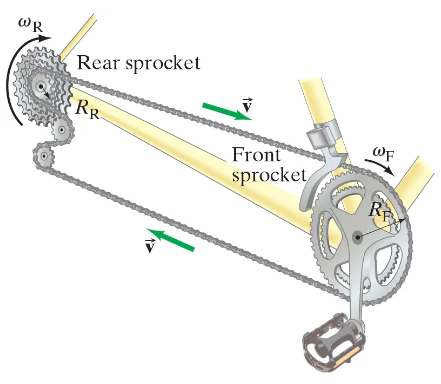
How is the angular velocity ωᵣ of the rear wheel of a bicycle related to the angular velocity ωբ of the front sprocket and pedals? Let Nբ and Nᵣ be the number of teeth on the front and rear sprockets, respectively, Fig. 10–71, and Rբ and Rᵣ their respective radii. The teeth are spaced the same on both sprockets and the rear sprocket is firmly attached to the rear wheel.

How is the angular velocity ωᵣ of the rear wheel of a bicycle related to the angular velocity ωբ of the front sprocket and pedals? Let Nբ and Nᵣ be the number of teeth on the front and rear sprockets, respectively, Fig. 10–71, and Rբ and Rᵣ their respective radii. The teeth are spaced the same on both sprockets and the rear sprocket is firmly attached to the rear wheel. Evaluate the ratio ωᵣ / ωբ when the front and rear sprockets have 52 and 13 teeth, respectively.

Bicycle gears:How is the angular velocity ωᵣ of the rear wheel of a bicycle related to the angular velocity ωբ of the front sprocket and pedals? Let Nբ and Nᵣ be the number of teeth on the front and rear sprockets, respectively, Fig. 10–71, and Rբ and Rᵣ their respective radii. The teeth are spaced the same on both sprockets and the rear sprocket is firmly attached to the rear wheel. Evaluate the ratio ωᵣ / ωբ when the front and rear sprocketshave 42 and 28 teeth.

A hollow cylinder (hoop) is rolling on a horizontal surface at speed v = 3.0 m/s when it reaches an 18° incline. How far up the incline will it go?

The density (mass per unit length) of a thin rod of length ℓ increases uniformly from λ₀ at one end to 3λ₀ at the other end. Determine the moment of inertia about an axis perpendicular to the rod through its geometric center.

A 5.0-m-long ladder is leaning against the side of a building making a 35° angle with the building. When a person is about 1/3 of the way up, the ladder slips and falls to the ground in 3.0 s. What is the average angular acceleration of the ladder as it falls?

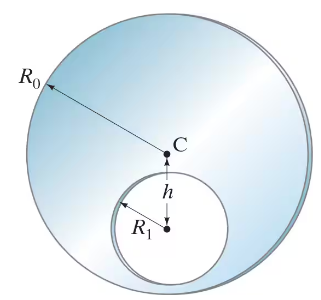
A crucial part of a piece of machinery starts as a flat uniform cylindrical disk of radius R₀ and mass M. It then has a circular hole of radius R₁ drilled into it (Fig. 10–80). The hole’s center is a distance h from the center of the disk. Find the moment of inertia of this disk (with off-center hole) when rotated about its center, C. [Hint: Consider a solid disk and “subtract” the hole; use the parallel-axis theorem.]

A cord connected at one end to a block which can slide on an inclined plane has its other end wrapped around a cylinder resting in a depression at the top of the plane as shown in Fig. 10–81. Determine the speed of the block after it has traveled 1.80 m along the plane, starting from rest. Assume there is no friction.