Back
BackProblem 2
A 7150-kg railroad car travels alone on a level frictionless track with a constant speed of 15.0 m/s. A 3650-kg load, initially at rest, is dropped onto the car. What will be the car’s new speed?
Problem 10
A 22-g bullet traveling 240 m/s penetrates a 2.0-kg block of wood and emerges going 130 m/s. If the block is stationary on a frictionless surface when hit, how fast does it move after the bullet emerges?
Problem 15
A mass mₐ = 2.0 kg, moving with velocity = (4.0 î + 5.0 ĵ ― 2.0 k̂) m/s, collides with mass m₈ = 3.0 kg, which is initially at rest. Immediately after the collision, mass mₐ is observed traveling at velocity = (― 2.0 î + 3.0 k̂) m/s. Find the velocity of mass m₈ after the collision. Assume no outside force acts on the two masses during the collision.
Problem 17a
A 195-kg projectile, fired with a speed of 116 m/s at a 60.0° angle, breaks into three pieces of equal mass at the highest point of its arc (where its velocity is horizontal). Two of the fragments move with the same speed right after the explosion as the entire projectile had just before the explosion; one of these moves vertically downward and the other horizontally. Determine the velocity of the third fragment immediately after the explosion.
Problem 24a
The force on a bullet along the barrel of a firearm is given by the formula F = [740 ― (2.3 x 10⁵ s⁻¹ ) t] N over the time interval t = 0 to t = 3.0 x 10⁻³ s. Plot a graph of F versus t for t = 0 to t = 3.0 ms.
Problem 24b
The force on a bullet along the barrel of a firearm is given by the formula F = [740 ― (2.3 x 10⁵ s⁻¹ ) t] N over the time interval t = 0 to t = 3.0 x 10⁻³ s. Plot a graph of F versus t for t = 0 to t = 3.0 ms. Use the graph to estimate the impulse given the bullet.
Problem 41
Croquet ball A moving at 4.3 m/s makes a head-on collision with ball B of equal mass initially at rest. Immediately after the collision, ball B moves forward at 3.0 m/s. What fraction of the initial kinetic energy is lost in the collision?
Problem 42a
A 144-g baseball moving 28.0 m/s strikes a stationary 4.85-kg brick resting on small rollers so it moves without significant friction. After hitting the brick, the baseball bounces straight back, and the brick moves forward at 1.10 m/s. What is the baseball’s speed after the collision?
Problem 42b
A 144-g baseball moving 28.0 m/s strikes a stationary 4.85-kg brick resting on small rollers so it moves without significant friction. After hitting the brick, the baseball bounces straight back, and the brick moves forward at 1.10 m/s. Find the total kinetic energy before and after the collision.
Problem 44
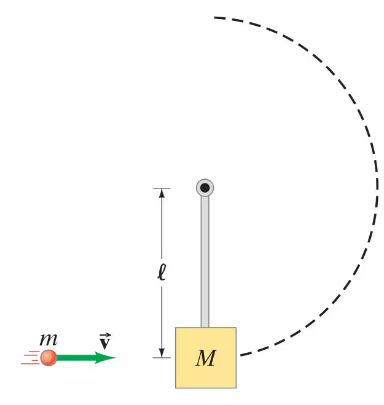
(II) A pendulum consists of a mass M hanging at the bottom end of a massless rod of length ℓ, which has a frictionless pivot at its top end. A mass m, moving horizontally as shown in Fig. 9–44 with velocity v, impacts M and becomes embedded. What is the smallest value of v sufficient to cause the pendulum (with embedded mass m) to swing clear over the top of its arc?
Problem 45b
A bullet of mass m = 0.0010 kg embeds itself in a wooden block with mass M = 0.999 kg, which then compresses a spring (k = 140 N/m) by a distance 𝓍 = 0.050 m before coming to rest. The coefficient of kinetic friction between the block and table is μ = 0.50. What fraction of the bullet’s initial kinetic energy is dissipated (in damage to the wooden block, rising temperature, etc.) in the collision between the bullet and the block?
Problem 54
The distance between a carbon atom (m = 12 u) and an oxygen atom (m = 16 u) in the CO molecule is 1.13 x 10⁻¹⁰ m. How far from the carbon atom is the center of mass of the molecule?
Problem 58
Find the center of mass of the ammonia molecule. The chemical formula is NH₃. The hydrogens are at the corners of an equilateral triangle (with sides 0.16 nm) that forms the base of a pyramid, with nitrogen at the apex (0.037 nm vertically above the plane of the triangle).
Problem 70a
A huge balloon and its gondola, of mass M, are in the air and stationary with respect to the ground. A passenger, of mass m, then climbs out and slides down a rope with speed v, measured with respect to the balloon. With what speed and direction (relative to Earth) does the balloon then move? What happens if the passenger stops?
Problem 73
A rocket traveling 1950 m/s away from the Earth at an altitude of 6400 km fires its rockets, which eject gas at a speed of 1200 m/s (relative to the rocket). If the mass of the rocket at this moment is 25,000 kg and an acceleration of 1.5 m/s² is desired, at what rate must the gases be ejected?
Problem 77
A 0.145-kg baseball pitched horizontally at 35.0 m/s strikes a bat and pops straight up to a height of 31.5 m. If the contact time between bat and ball is 2.5 ms, calculate the average force between the ball and bat during contact.
Problem 80
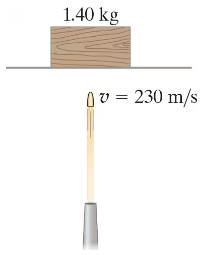
A gun fires a bullet vertically into a 1.40-kg block of wood at rest on a thin horizontal sheet, Fig. 9–54. If the bullet has a mass of 15.0 g and a speed of 230 m/s, how high will the block rise into the air after the bullet becomes embedded in it?
Problem 85a
A 5.5-kg object moving in the +𝓍 direction at 6.5 m/s collides head-on with an 8.0-kg object moving in the ―𝓍 direction at 4.0 m/s. Determine the final velocity of each object if the objects stick together.
Problem 85b
A 5.5-kg object moving in the +𝓍 direction at 6.5 m/s collides head-on with an 8.0-kg object moving in the ―𝓍 direction at 4.0 m/s. Determine the final velocity of each object if the collision is elastic.
Problem 85c
A 5.5-kg object moving in the +𝓍 direction at 6.5 m/s collides head-on with an 8.0-kg object moving in the ―𝓍 direction at 4.0 m/s. Determine the final velocity of each object if the 5.5-kg object is at rest after the collision.
Problem 92
A rifle is aimed at a 2.0-kg block of wood along an inclined plane making an angle of 25°, as shown in Fig. 9–59. A 9.5-g bullet is fired at 760 m/s and becomes embedded in the block. How far up the incline does the block/bullet slide?
(a) Ignore the friction.
(b) Assume μₖ = 0.33.
Problem 93a
Astronomers estimate that a 2.0-km-diameter asteroid collides with the Earth once every million years. The collision could pose a threat to life on Earth. Assume a spherical asteroid has a mass of 3200 kg for each cubic meter of volume and moves toward the Earth at 15 km/s. How much destructive energy could be released when it embeds itself in the Earth?
Problem 94
An astronaut of mass 210 kg including his suit and jet pack wants to acquire a velocity of 2.0 m/s to move back toward his space shuttle. Assuming the jet pack can eject gas with a velocity of 35 m/s, what mass of gas will need to be ejected?
Problem 96
A fake hockey puck of mass 4m has been rigged to explode. Initially the puck is at rest on a frictionless ice rink. Then it bursts into three pieces. One chunk, of mass m, slides across the ice at velocity vî. Another chunk, of mass 2m, slides across the ice at velocity 2v ĵ. Determine the velocity of the third chunk.
Problem 100
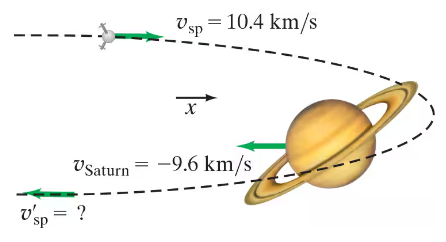
The gravitational slingshot effect. Figure 9–62 shows the planet Saturn moving in the negative 𝓍 direction at its orbital speed (with respect to the Sun) of 9.6 km/s. The mass of Saturn is 5.69 x 10²⁶ kg. A spacecraft with mass 825 kg approaches Saturn. When far from Saturn, it moves in the +𝓍 direction at 10.4 km/s. The gravitational attraction of Saturn (a conservative force) acting on the spacecraft causes it to swing around the planet (orbit shown as dashed line) and head off in the opposite direction. Using momentum conservation in one dimension, estimate the final speed of the spacecraft after it is far enough away to be considered free of Saturn’s gravitational pull. Assume the spacecraft does not affect the orbit of Saturn whose mass is so much larger.
Problem 103a
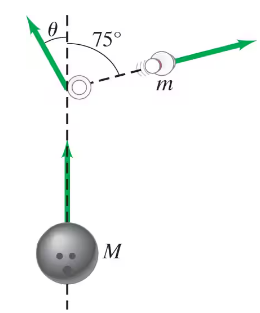
In order to convert a tough split in bowling, it is necessary to strike the pin a glancing blow as shown in Fig. 9–64. Assume that the bowling ball, traveling at 14.0 m/s just before it strikes the pin, has five times the mass of a pin and that the pin goes off at 75° from the original direction of the ball. Calculate the speed of the pin and (b) of the ball just after collision.