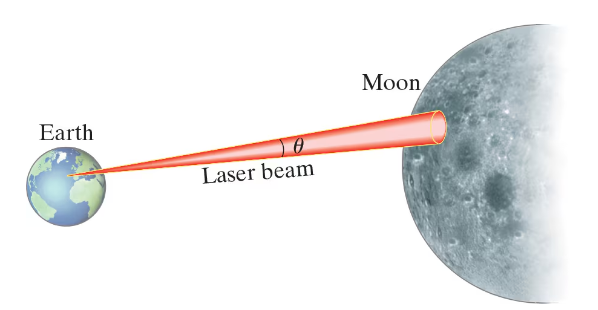
(I) A laser beam is directed at the Moon, 380,000 km from Earth. The beam diverges at an angle θ (Fig. 10–50) of 1.4 x 10^-5 rad. What diameter spot will it make on the Moon?

The platter of the hard drive of a computer rotates at 7200 rpm (rpm = revolutions per minute = rev/min). What is the angular velocity (rad/s) of the platter?

The platter of the hard drive of a computer rotates at 7200 rpm (rpm = revolutions per minute = rev/min). If the reading head of the drive is located 3.00 cm from the rotation axis, what is the linear speed of the point on the platter just below it?

The platter of the hard drive of a computer rotates at 7200 rpm (rpm = revolutions per minute = rev/min). If a single bit requires 0.50 μm of length along the direction of motion, how many bits per second can the writing head write when it is 3.00 cm from the axis?

A child rolls a ball on a level floor 3.1 m to another child. If the ball makes 12.0 revolutions, what is its diameter?

(II) A child rolls a ball on a level floor 3.1 m to another child. If the ball makes 12.0 revolutions, what is its diameter?

How fast (in rpm) must a centrifuge rotate if a particle 8.0 cm from the axis of rotation is to experience an acceleration of 100,000 g’s?

A turntable of radius R₁ is turned by a circular rubber roller of radius R₂ in contact with it at their outer edges. What is the ratio of their angular velocities, ω₁/ω₂?

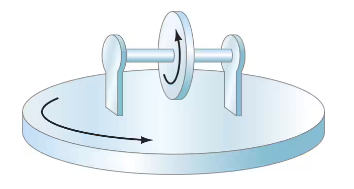
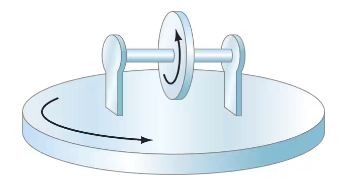
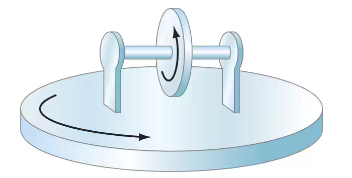
The axle of a wheel is mounted on supports that rest on a rotating turntable as shown in Fig. 10–52. The wheel has angular velocity ω₁ = 48.0 rad/s about its axle, and the turntable has angular velocity ω₂ = 35.0 rad/s about a vertical axis. (Note arrows showing these motions in the figure.) What are the directions of $\overrightarrow{{\omega }_1}$ and $\overrightarrow{{\omega }_2}$ at the instant shown?

The axle of a wheel is mounted on supports that rest on a rotating turntable as shown in Fig. 10–52. The wheel has angular velocity ω₁ = 48.0 rad/s about its axle, and the turntable has angular velocity ω₂ = 35.0 rad/s about a vertical axis. (Note arrows showing these motions in the figure? What is the resultant angular velocity of the wheel, as seen by an outside observer, at the instant shown? Give the magnitude and direction.

The axle of a wheel is mounted on supports that rest on a rotating turntable as shown in Fig. 10–52. The wheel has angular velocity ω₁ = 48.0 rad/s about its axle, and the turntable has angular velocity ω₂ = 35.0 rad/s about a vertical axis. (Note arrows showing these motions in the figure.) What is the magnitude and direction of the angular acceleration of the wheel at the instant shown? Take the 𝒵 axis vertically upward and the direction of the axle at the moment shown to be the 𝓍 axis pointing to the right.

Pilots can be tested for the stresses of flying high-speed jets in a whirling “human centrifuge,” which takes 1.0 min to turn through 26 complete revolutions before reaching its final speed. What was its final angular speed in rpm?

The angular acceleration of a wheel, as a function of time, is α = 4.2 t² ― 9.0 t , where α is in rad/s² and t in seconds. If the wheel starts from rest (θ = 0 , ω = 0, at t = 0), determine a formula for the angular position θ, both as a function of time.

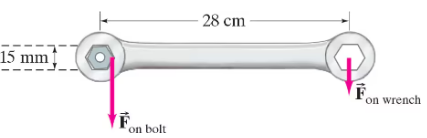
The bolts on the cylinder head of an engine require tightening to a torque of 95 m-N. If the six-sided bolt head is 15 mm across (Fig. 10–55), estimate the force applied near each of the six points by a wrench.

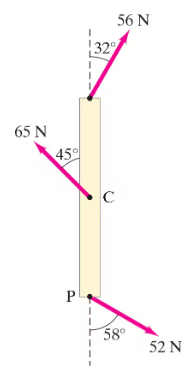
Determine the net torque on the 2.0-m-long uniform beam shown in Fig. 10–56. All forces are shown. Calculate about point P at one end.

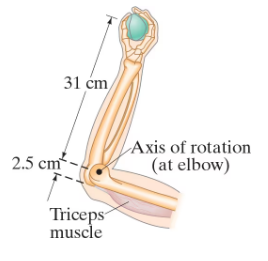
The forearm in Fig. 10–57 accelerates a 3.6-kg ball at 7.0 m/s² by means of the triceps muscle, as shown. Calculate the torque needed.

A softball player swings a bat, accelerating it from rest to 2.4 rev/s in a time of 0.20 s. Approximate the bat as a 0.90-kg uniform rod of length 0.95 m, and compute the torque the player applies to one end of it.

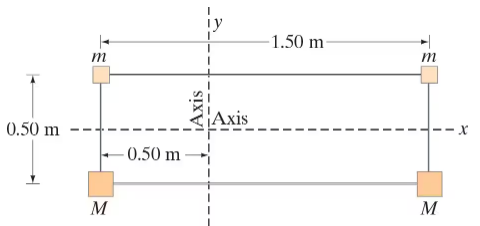
Calculate the moment of inertia of the array of point objects shown in Fig. 10–58 about the y axis, and the x axis. Assume m = 22kg, M = 3.2kg, and the objects are wired together by very light, rigid pieces of wire. The array is rectangular and is split through the middle by the x axis. About which axis would it be harder to accelerate this array?

A dad pushes tangentially on a small hand-driven merry-go-round and is able to accelerate it from rest to a frequency of 15 rpm in 10.0 s. Assume the merry-go-round is a uniform disk of radius 2.5 m and has a mass of 330 kg, and two children (each with a mass of 25 kg) sit opposite each other on the edge. Calculate the torque required to produce the acceleration, neglecting frictional torque. What force is required at the edge?

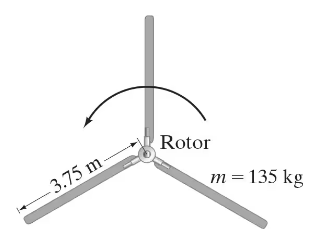
Let us treat a helicopter rotor blade as a long thin rod, as shown in Fig. 10–60. If each of the three rotor helicopter blades is 3.75 m long and has a mass of 135 kg, calculate the moment of inertia of the three rotor blades about the axis of rotation.

Suppose the force Fₜ in the cord hanging from the pulley of Example 10–10, Fig. 10–22, is given by the relation Fₜ = 3.00 t ― 0.20 t² (newtons) where t is in seconds. If the pulley starts from rest, what is the linear speed of a point on its rim 9.0 s later? Ignore friction and use the moment of inertia, calculated in Example 10–10.

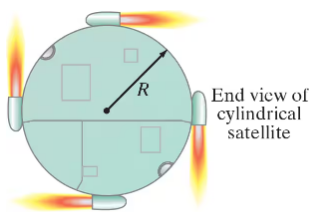
To get a flat, uniform cylindrical satellite spinning at the correct rate, engineers fire four tangential rockets as shown in Fig. 10–61. Suppose that the satellite has a mass of 3600 kg and a radius of 4.0 m, and that the rockets each add a mass of 250 kg. What is the steady force required of each rocket if the satellite is to reach 28 rpm in 5.0 min, starting from rest?

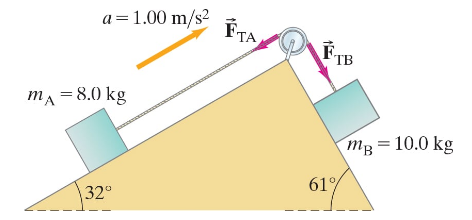
Two blocks are connected by a light string passing over a pulley of radius 0.15 m and moment of inertia I. The blocks move (towards the right) with an acceleration of 1.00 m/s² along their frictionless inclines (see Fig. 10–62). Find the net torque acting on the pulley, and determine its moment of inertia, I.

(III) Integrate to derive the formula for the moment of inertia of a uniform thin rod of length ℓ about an axis through its center, perpendicular to the rod (see Fig. 10–21f).

A 2.30-m-long pole is balanced vertically on its tip. It starts to fall and its lower end does not slip. What will be the speed of the upper end of the pole just before it hits the ground? [Hint: Use conservation of energy.]

A bowling ball of mass 7.3 kg and radius 9.0 cm rolls without slipping down a lane at 3.7 m/s. Calculate its total kinetic energy.

II) A uniform solid sphere of radius r₀ = 24.5 cm and mass m = 1.60 kg starts from rest and rolls without slipping down a 30.0° incline that is 10.0 m long. Calculate its translational and rotational speeds when it reaches the bottom. Avoid putting in numbers until the end so you can answer.

A solid rubber ball rests on the floor of a railroad car when the car begins moving with acceleration a. Assuming the ball rolls without slipping, what is its acceleration relative to the car?

A solid rubber ball rests on the floor of a railroad car when the car begins moving with acceleration a. Assuming the ball rolls without slipping, what is its acceleration relative to the ground?

The 1100-kg mass of a car includes four tires, each of mass 35 kg (including wheels) and diameter 0.80 m. Assume each tire and wheel combination acts as a solid cylinder. Determine the total kinetic energy of the car when traveling 95 km/h.