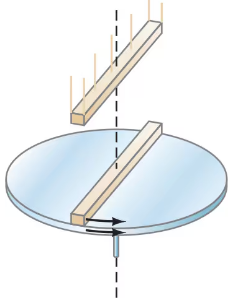
A uniform disk turns at 4.1 rev/s around a frictionless central axis. A nonrotating rod, of the same mass as the disk and length equal to the disk’s diameter, is dropped onto the freely spinning disk, Fig. 11–32. They then turn together around the spindle with their centers superposed. What is the angular frequency in rev/s of the combination?

A person of mass 75 kg stands at the center of a rotating merry-go-round platform of radius 3.0 m and moment of inertia 920. kg·m². The platform rotates without friction with angular velocity 0.95 rad/s. The person walks radially to the edge of the platform. Calculate the rotational kinetic energy of the system of platform plus person before and after the person’s walk.

A woman of mass m stands at the edge of a solid cylindrical platform of mass M and radius R. At t = 0, the platform is rotating with negligible friction at angular velocity ω₀ about a vertical axis through its center, and the woman begins walking with speed υ (relative to the platform) toward the center of the platform. Determine the angular velocity of the system as a function of time.

A woman of mass m stands at the edge of a solid cylindrical platform of mass M and radius R. At t = 0, the platform is rotating with negligible friction at angular velocity ω₀ about a vertical axis through its center, and the woman begins walking with speed υ (relative to the platform) toward the center of the platform. What will be the angular velocity when the woman reaches the center?

Show that  î x ĵ = k̂ , î x k̂ = - ĵ, and ĵ x k̂ = î.

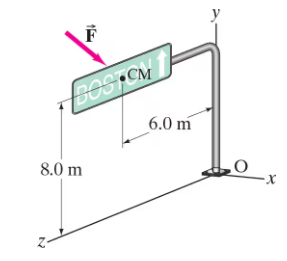
An engineer estimates that under the most adverse expected weather conditions, the total force on the highway sign in Fig. 11–33 will be $\overrightarrow{F}$ = (± 2.4 î - 4.1 ĵ) kN, acting at the cm. What torque does this force exert about the base O?

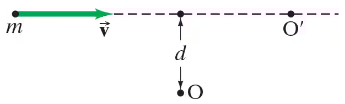
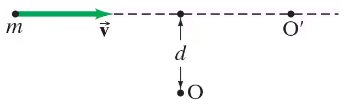
Calculate the angular momentum of a particle of mass m moving with constant velocity υ for two cases (see Fig. 11–34): about origin O.

Calculate the angular momentum of a particle of mass m moving with constant velocity υ for two cases (see Fig. 11–34): about O′.

Two identical particles have equal but opposite momenta, $\overrightarrow{p}$ and $-\overrightarrow{p}$, but they are not traveling along the same line. Show that the total angular momentum of this system does not depend on the choice of origin.

A particle is at the position (x, y, z) = (1.0, 2.0, 3.0)m. It is traveling with a vector velocity (-5.0 ,+ 2.8, -3.1)m/s. Its mass is 4.3 kg. What is its vector angular momentum about the origin?

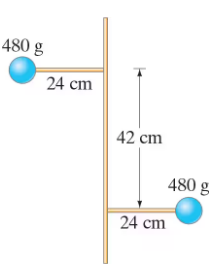
Two lightweight rods 24 cm in length are mounted perpendicular to an axle and at 180° to each other (Fig. 11–35). At the end of each rod is a 480-g mass. The rods are spaced 42 cm apart along the axle. The axle rotates at 4.5 rad/s.

(a) What is the component of the total angular momentum along the axle?

(b) What angle does the vector angular momentum make with the axle? [Hint: Remember that the vector angular momentum must be calculated about the same point for both masses, which could be the cm.]

Two ice skaters, both of mass 68 kg, approach on parallel paths 1.6 m apart. Both are moving at 3.5 m/s with their arms outstretched. They join hands as they pass, still maintaining their 1.6-m separation, and begin rotating about one another. Treat the skaters as particles with regard to their rotational inertia. Calculate the change in kinetic energy for this process.

Two ice skaters, both of mass 68 kg, approach on parallel paths 1.6 m apart. Both are moving at 3.5 m/s with their arms outstretched. They join hands as they pass, still maintaining their 1.6-m separation, and begin rotating about one another. Treat the skaters as particles with regard to their rotational inertia. If they now pull on each other’s hands, reducing their radius to half its original value, what is their common angular speed after reducing their radius?

Two ice skaters, both of mass 68 kg, approach on parallel paths 1.6 m apart. Both are moving at 3.5 m/s with their arms outstretched. They join hands as they pass, still maintaining their 1.6-m separation, and begin rotating about one another. Treat the skaters as particles with regard to their rotational inertia. They now pull on each other’s hands, reducing their radius to half its original value. Calculate the change in kinetic energy for this process.

Suppose a 5.2 x 10¹⁰kg meteorite struck the Earth at the equator with a speed v = 2.2 x 10⁴ m/s, as shown in Fig. 11–38 and remained stuck. By what factor would this affect the rotational frequency of the Earth (1 rev/day)?

<IMAGE>

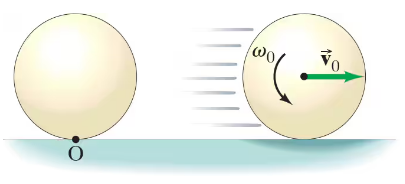
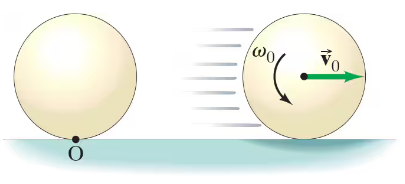
On a level billiards table a cue ball, initially at rest at point O on the table, is struck so that it leaves the cue stick with a center-of-mass speed v₀ and ω₀ a “reverse” spin of angular speed (see Fig. 11–41). A kinetic friction force acts on the ball as it initially skids across the table. Using conservation of angular momentum, find the critical angular speed ω_C such that, if ω₀=ω_C, kinetic friction will bring the ball to a complete (as opposed to momentary) stop.

On a level billiards table a cue ball, initially at rest at point O on the table, is struck so that it leaves the cue stick with a center-of-mass speed v₀ and ω₀ a “reverse” spin of angular speed (see Fig. 11–41). A kinetic friction force acts on the ball as it initially skids across the table. If ω₀ is 10% smaller than ω_C , i.e., ω₀ = 0.90ω_C, determine the ball’s cm velocity v_CM when it starts to roll without slipping.

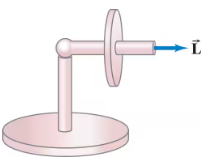
A toy gyroscope consists of a 170-g disk with a radius of 5.5 cm mounted at the center of a thin axle 21 cm long (Fig. 11–42). The gyroscope spins at 45 rev/s. One end of its axle rests on a stand and the other end precesses horizontally about the stand. How long does it take the gyroscope to precess once around?

Suppose the solid wheel of Fig. 11–42 has a mass of 260 g and rotates at 85 rad/s; it has radius 6.0 cm and is mounted at the center of a horizontal thin axle 25 cm long. At what rate does the axle precess?

A merry-go-round with a moment of inertia equal to 860 kg·m² and a radius of 3.0 m rotates with negligible friction at 1.70 rad/s. A child initially standing still next to the merry-go-round jumps onto the edge of the platform straight toward the axis of rotation causing the platform to slow to 1.25 rad/s. What is her mass?

The time-dependent position of a point object which moves counterclockwise along the circumference of a circle (radius R) in the xy plane with constant speed υ is given by $\overrightarrow{r}$ = î R cos ωt + ĵ R sin ωt where the constant ω = v/R. Determine the velocity $\overrightarrow{v}$ and angular velocity $\overrightarrow{w}$ of this object and then show that these three vectors obey the relation$\overrightarrow{v}=\overrightarrow{\omega }\times \overrightarrow{r}$.

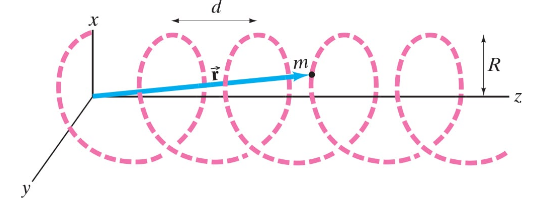
The position of a particle with mass m traveling on a helical path (see Fig. 11–48) is given by $\overrightarrow{r}$ = R cos (2πz/d) î + R sin (2πz/d) ĵ + zk̂ where R and d are the radius and pitch of the helix, respectively, and z has time dependence z = v_𝓏t where v_𝓏 is the (constant) component of velocity in the z direction. Determine the time-dependent angular momentum $\overrightarrow{L}$ of the particle about the origin.

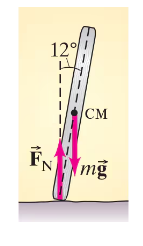
A boy rolls a tire along a straight level street. The tire has mass 8.0 kg, radius 0.32 m and moment of inertia about its central axis of symmetry of 0.83 kg·m². The boy pushes the tire forward away from him at a speed of 2.1 m/s and sees that the tire leans 12° to the right (Fig. 11–49). How will the resultant torque due to gravity and the normal force $\overrightarrow{F_N}$ affect the subsequent motion of the tire? 

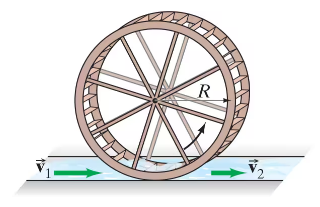
Water drives a waterwheel (or turbine) of radius R = 3.0 m as shown in Fig. 11–50. The water enters at a speed v₁ = 7.0m/s and exits from the waterwheel at a speed v₂= 3.8 m/s. If the water causes the waterwheel to make one revolution every 6.0 s, how much power is delivered to the wheel?

A particle of mass m uniformly accelerates as it moves counterclockwise along the circumference of a circle of radius R: $\overrightarrow{r}$ = î R cos θ + ĵ R sin θ with θ = ω₀t + (1/2)αt² , where the constants ω₀ and α are the initial angular velocity and angular acceleration, respectively. Determine the object’s tangential acceleration $\overrightarrow{a}$_tan and determine the torque acting on the object using $\overrightarrow{\tau }=\overrightarrow{r}\times F$.

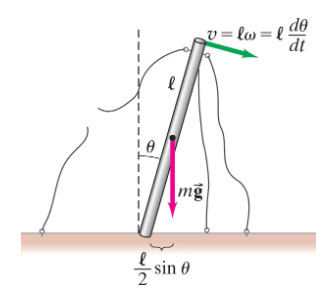
A radio transmission tower has a mass of 76 kg and is 12 m high. The tower is anchored to the ground by a flexible joint at its base, but it is secured by three cables 120° apart (Fig. 11–52). In an analysis of a potential failure, a mechanical engineer needs to determine the behavior of the tower if one of the cables breaks. The tower would fall away from the broken cable, rotating about its base. Determine the speed of the top of the tower as a function of the rotation angle θ. Start your analysis with the rotational dynamics equation of motion d$\overrightarrow{L}$/dt =${\overrightarrow{{\tau }_{ext}}}_{}$. Approximate the tower as a tall thin rod.

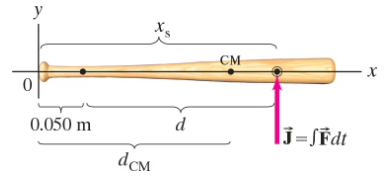
A baseball bat has a sweet spot where a ball can be hit with almost effortless transmission of energy. A careful analysis of baseball dynamics shows that this special spot is located at the point where an applied force would result in pure rotation of the bat about the handle grip. Determine the location of the sweet spot, xₛ, of the bat shown in Fig. 11–53. The linear mass density of the bat is given roughly by (0.61 + 3.3x²) kg/m, where x is in meters measured from the end of the handle. The entire bat is 0.84 m long. The desired rotation point should be 5.0 cm from the thin end where the bat is held. [Hint: Where is the cm of the bat?]