In their study of X-ray diffraction, William and Lawrence Bragg determined that the relationship among the wavelength of the radiation 1l2, the angle at which the radiation is diffracted 1u2, and the distance between planes of atoms in the crystal that cause the diffraction (d) is given by nl = 2d sin u. X rays from a copper X-ray tube that have a wavelength of 1.54 Å are diffracted at an angle of 14.22 degrees by crystalline silicon. Using the Bragg equation, calculate the distance between the planes of atoms responsible for diffraction in this crystal, assuming n = 1 (first-order diffraction).
Ch.12 - Solids and Modern Materials

Brown15th EditionChemistry: The Central ScienceISBN: 9780137542970Not the one you use?Change textbook
Chapter 12, Problem 119b
(b) X-ray diffraction studies of buckminsterfullerene show that it has a face-centered cubic lattice of C60 molecules. The length of an edge of the unit cell is 14.2 Å. Calculate the density of buckminsterfullerene.
 Verified step by step guidance
Verified step by step guidance1
Identify the type of lattice structure: Buckminsterfullerene has a face-centered cubic (FCC) lattice structure.
Determine the number of C60 molecules per unit cell in an FCC lattice: An FCC lattice has 4 atoms or molecules per unit cell.
Calculate the molar mass of a C60 molecule: The molar mass of carbon (C) is approximately 12.01 g/mol. Therefore, the molar mass of C60 is 60 times the molar mass of carbon, which is 60 * 12.01 g/mol.
Convert the edge length of the unit cell from Ångströms to centimeters: 1 Å = 1 x 10^-8 cm, so 14.2 Å = 14.2 x 10^-8 cm.
Calculate the density using the formula: \( \text{Density} = \frac{\text{Mass of molecules in unit cell}}{\text{Volume of unit cell}} \). Use the molar mass, Avogadro's number, and the converted edge length to find the mass and volume.

Verified video answer for a similar problem:
This video solution was recommended by our tutors as helpful for the problem above.
Video duration:
4mWas this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Unit Cell and Lattice Structure
A unit cell is the smallest repeating unit in a crystal lattice that reflects the overall symmetry and structure of the entire crystal. In the case of buckminsterfullerene, it has a face-centered cubic (FCC) lattice, meaning that the unit cell is cubic with atoms located at each corner and the center of each face. Understanding the unit cell is crucial for calculating properties like density.
Recommended video:
Guided course
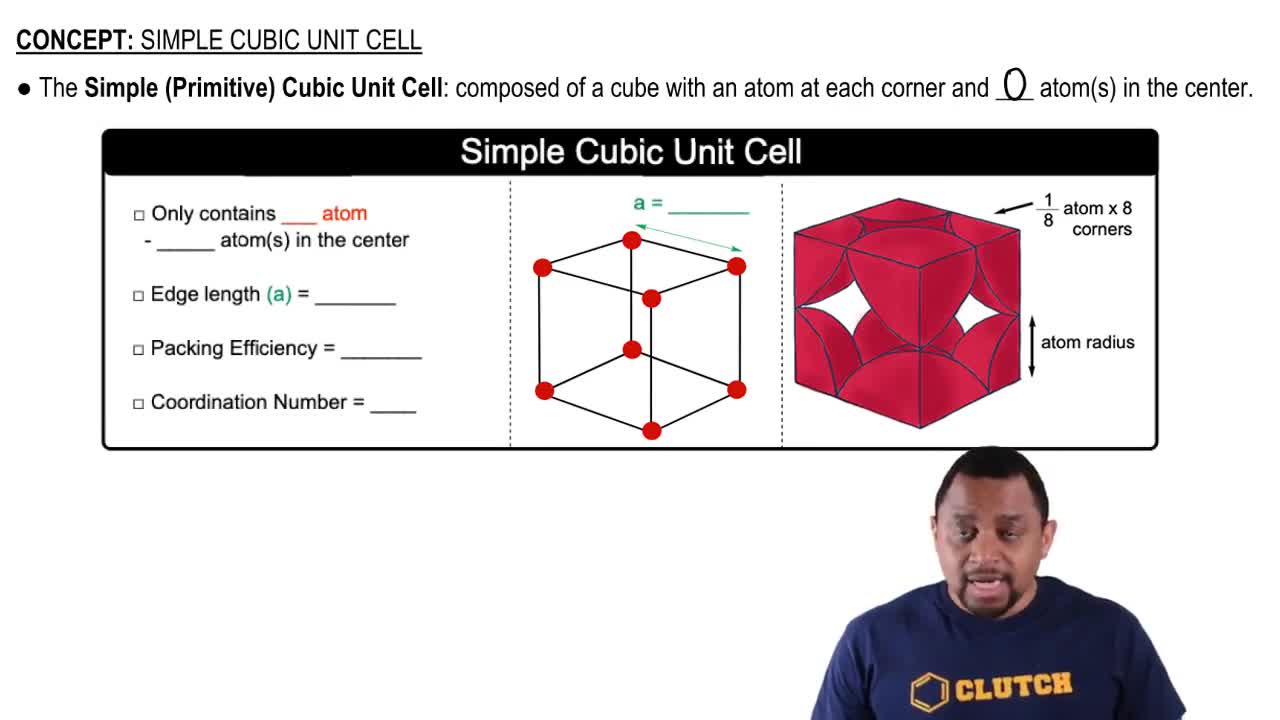
Simple Cubic Unit Cell
Density Calculation
Density is defined as mass per unit volume and is typically expressed in grams per cubic centimeter (g/cm³). To calculate the density of a substance, one must know the mass of the unit cell and its volume. For buckminsterfullerene, the volume can be determined from the edge length of the unit cell, while the mass can be calculated based on the number of C60 molecules in the unit cell.
Recommended video:
Guided course

Density Concepts
Molar Mass and Avogadro's Number
The molar mass of a substance is the mass of one mole of its entities, typically expressed in grams per mole (g/mol). For buckminsterfullerene (C60), the molar mass is approximately 720 g/mol. Avogadro's number (6.022 x 10²³) relates the number of molecules in a mole to its mass, allowing for the conversion between the mass of the unit cell and the number of molecules it contains, which is essential for density calculations.
Recommended video:
Guided course

Molar Mass Concept
Related Practice
Textbook Question
Textbook Question
Germanium has the same structure as silicon, but the unit cell size is different because Ge and Si atoms are not the same size. If you were to repeat the experiment described in Additional Exercise 12.117, but replace the Si crystal with a Ge crystal, would you expect the X rays to be diffracted at a larger or smaller angle 𝜃?
Textbook Question
(a) The density of diamond is 3.5 g/cm3, and that of graphite is 2.3 g/cm3. Based on the structure of buckminsterfullerene, what would you expect its density to be relative to these other forms of carbon?
Textbook Question
(a) What are the C—C—C bond angles in diamond?
1
views
