Factor $\text{ƒ}\left(x\right)$ into linear factors given that k is a zero. $\text{ƒ}\left(x\right)=2x^4+x^3-9x^2-13x-5;k=-1$ (multiplicity $3$)

Show that each polynomial function has a real zero as described in parts (a) and (b). In Exercises 31 and 32, also work part (c). ƒ(x)=4x³-37x²+50x+60 between 2 and 3

Show that each polynomial function has a real zero as described in parts (a) and (b). In Exercises 31 and 32, also work part (c). ƒ(x)=4x³-37x²+50x+60 between 7 and 8

Show that each polynomial function has a real zero as described in parts (a) and (b). In Exercises 31 and 32, also work part (c). ƒ(x)=4x^3-37x^2+50x+60 Find the zero in part (b) to three decimal places.

Solve each polynomial inequality. Give the solution set in interval notation. (x + 3)³(2x - 1)(x + 4) ≥ 0

Match the rational function in Column I with the appropriate description in Column II. Choices in Column II can be used only once. ƒ(x)=(x²-16)/(x+4)

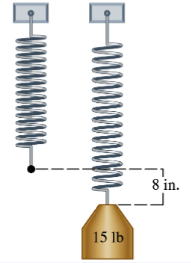
Hooke's Law for a Spring Hooke's law for an elastic spring states that the distance a spring stretches varies directly as the force applied. If a force of 15 lb stretches a certain spring 8 in., how much will a force of 30 lb stretch the spring?

For each polynomial function, use the remainder theorem to find ƒ(k). ƒ(x) = x² + 5x+6; k = -2

For each polynomial function, one zero is given. Find all other zeros. $\text{ƒ}\left(x\right)=x^3-x^2-4x-6;3$

Show that each polynomial function has a real zero as described in parts (a) and (b). In Exercises 31 and 32, also work part (c). ƒ(x)=6x^4+13x^3-11x^2-3x+5 no zero greater than 1

Show that each polynomial function has a real zero as described in parts (a) and (b). In Exercises 31 and 32, also work part (c). ƒ(x)=6x^4+13x^3-11x^2-3x+5 no zero less than -3

For each polynomial function, one zero is given. Find all other zeros. $\text{ƒ}\left(x\right)=x^3+4x^2-5;1$

Graph each polynomial function. Factor first if the polynomial is not in factored form. ƒ(x)=x²(x-5)(x+3)(x-1)

Solve each problem. Use Descartes' rule of signs to determine the different possibilities for the numbers of positive, negative, and nonreal complex zeros of $\text{ƒ}\left(x\right)=x^3+3x^2-4x-2$.

Graph each quadratic function. Give the (a) vertex, (b) axis, (c) domain, and (d) range. ƒ(x) = -3x² + 24x - 46

Graph each polynomial function. Factor first if the polynomial is not in factored form. ƒ(x)=(3x-1)(x+2)²

Match the rational function in Column I with the appropriate description in Column II. Choices in Column II can be used only once. ƒ(x)=(x²+3x+4)/(x-5)

Solve each problem. Is x+1 a factor of ƒ(x)=x³+2x²+3x+2?

For each polynomial function, use the remainder theorem to find ƒ(k). ƒ(x) = 2x² - 3x-3; k = 2

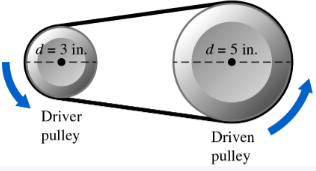
Solve each problem. The speed of a pulley varies inversely as its diameter. One kind of pulley, with diameter 3 in., turns at 150 revolutions per minute. Find the speed of a similar pulley with diameter 5 in.

For each polynomial function, use the remainder theorem to find ƒ(k). ƒ(x) = - x³ + 8x² + 63; k=4

Graph each polynomial function. Factor first if the polynomial is not in factored form. ƒ(x)=(4x+3)(x+2)²

For each polynomial function, one zero is given. Find all other zeros. $\text{ƒ}\left(x\right)=4x^3+6x^2-2x-1;\frac{1}{2}$

Solve each problem. Find a polynomial function ƒ of degree 3 with -2, 1, and 4 as zeros, and ƒ(2)=16.

For each polynomial function, use the remainder theorem to find ƒ(k). ƒ(x) = x³ - 4x² + 2x+1; k = -1

For each polynomial function, one zero is given. Find all other zeros. $\text{ƒ}\left(x\right)=-x^4-5x^2-4;-i$

Give the equations of any vertical, horizontal, or oblique asymptotes for the graph of each rational function. ƒ(x)=3/(x-5)

Determine the largest open interval of the domain (a) over which the function is increasing and (b) over which it is decreasing. ƒ(x) = (x + 3)²

Current Flow In electric current flow, it is found that the resistance offered by a fixed length of wire of a given material varies inversely as the square of the diameter of the wire. If a wire 0.01 in. in diameter has a resistance of 0.4 ohm, what is the resistance of a wire of the same length and material with diameter 0.03 in., to the nearest ten-thousandth of an ohm?

Graph each polynomial function. Factor first if the polynomial is not in factored form. ƒ(x)=x³+5x²-x-5