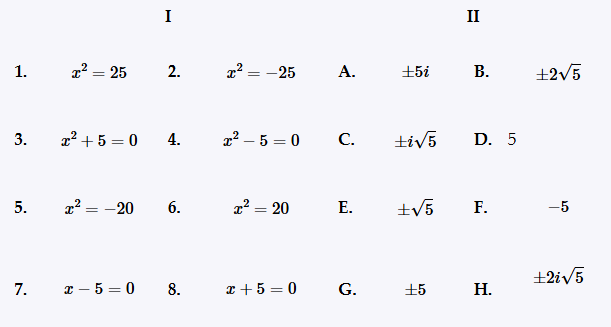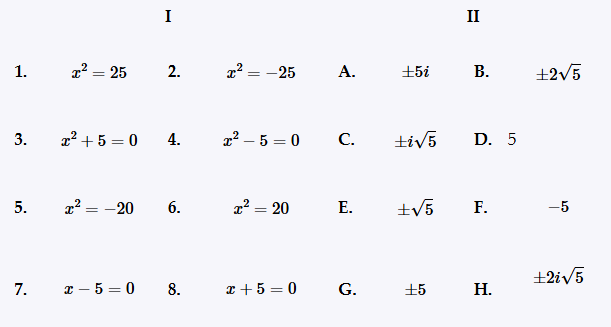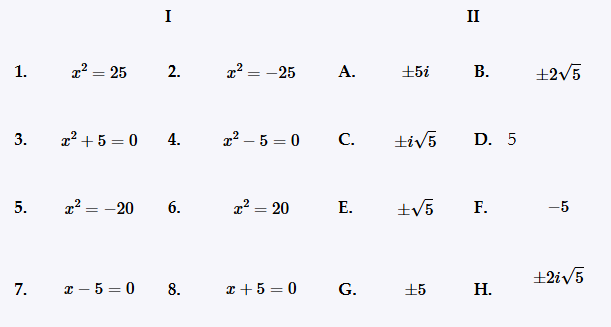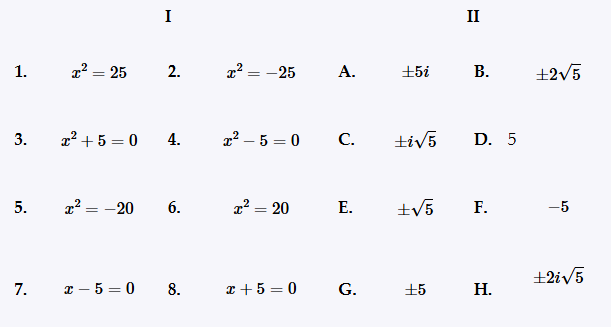Back
BackProblem 1
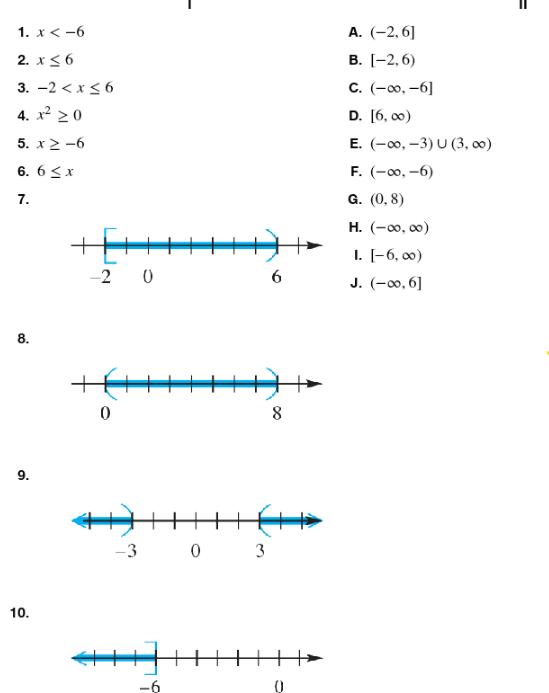
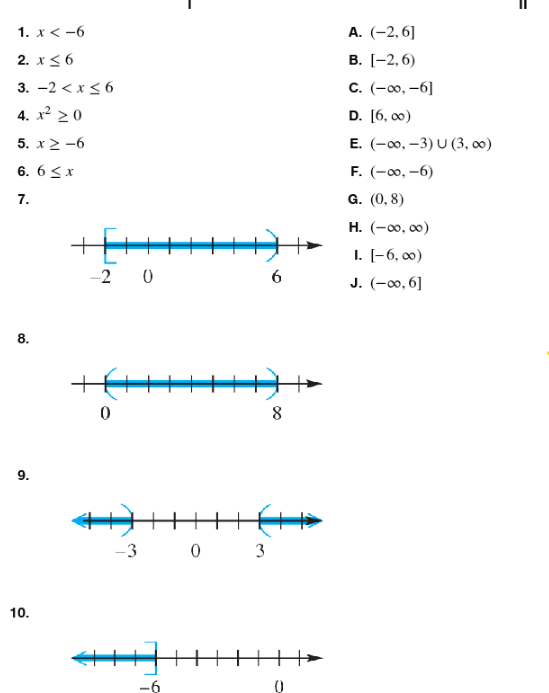
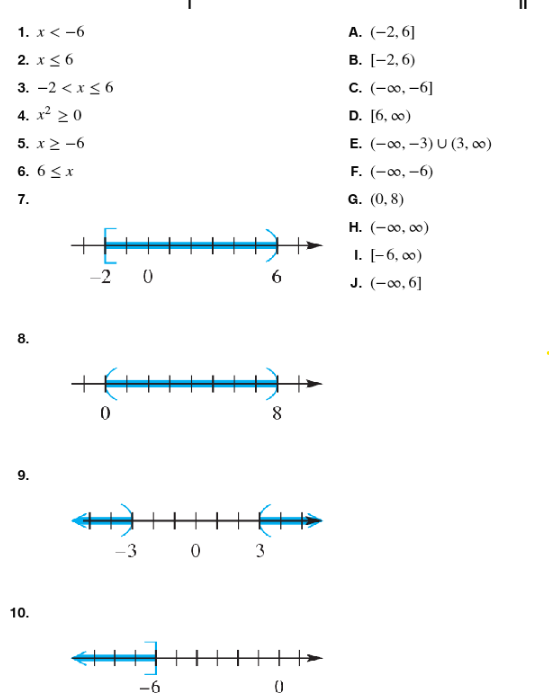
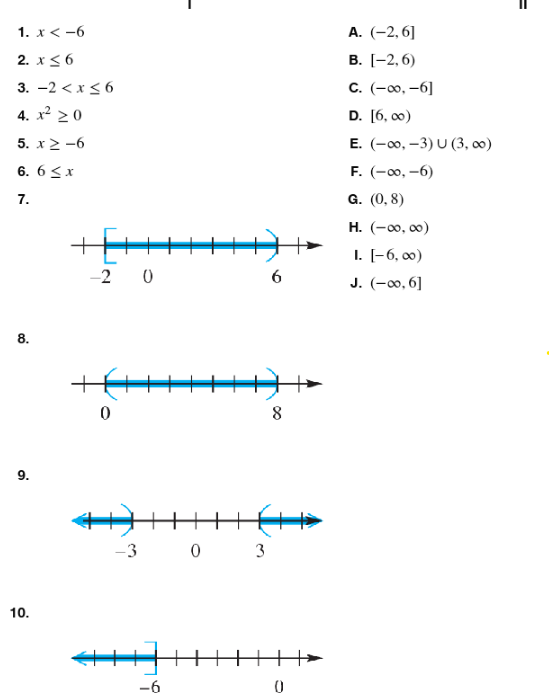
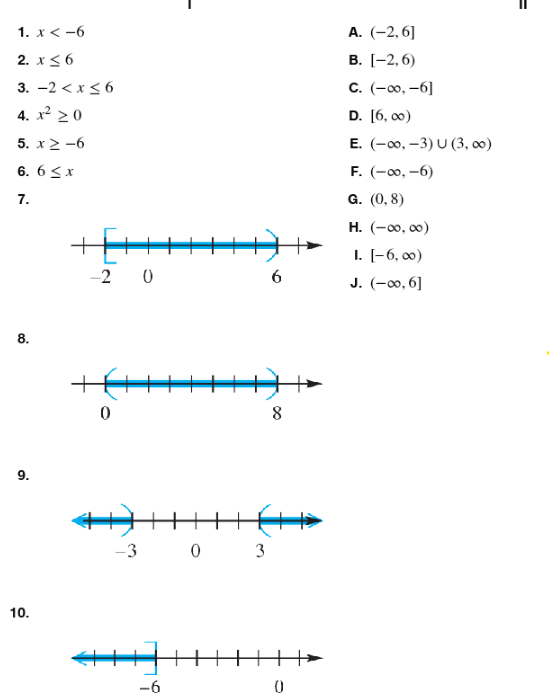
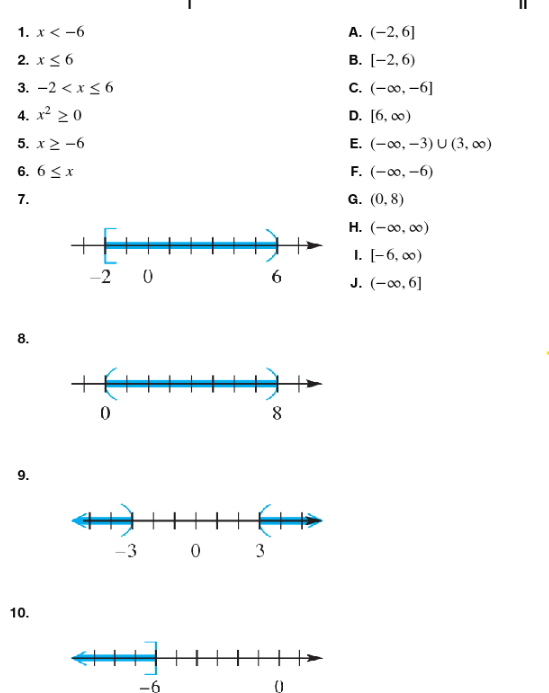
Match the inequality in each exercise in Column I with its equivalent interval notation in Column II. x<-6
Problem 1
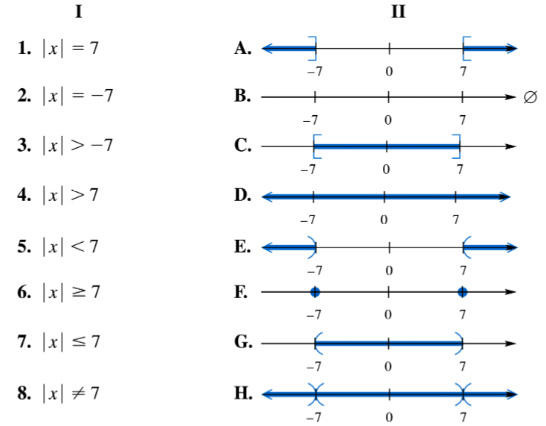
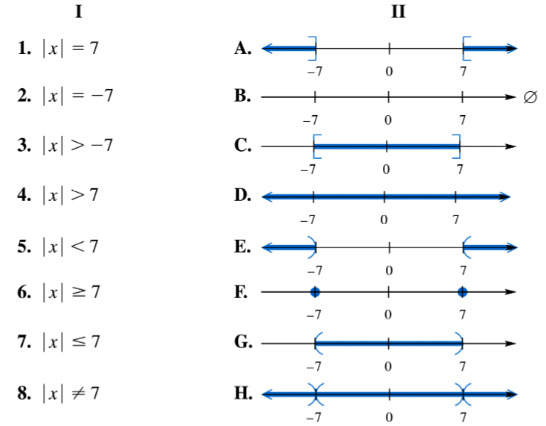
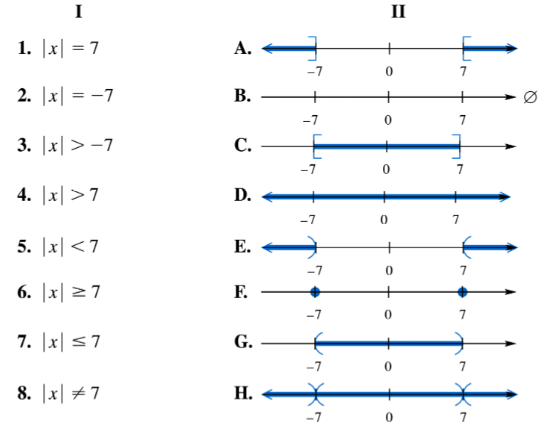
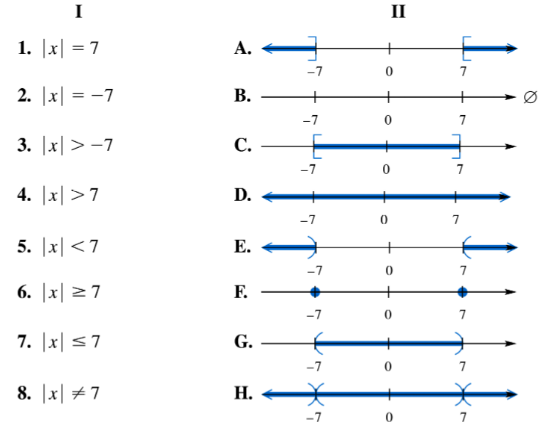
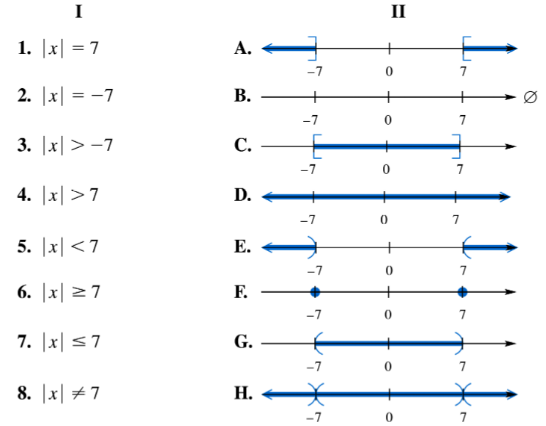
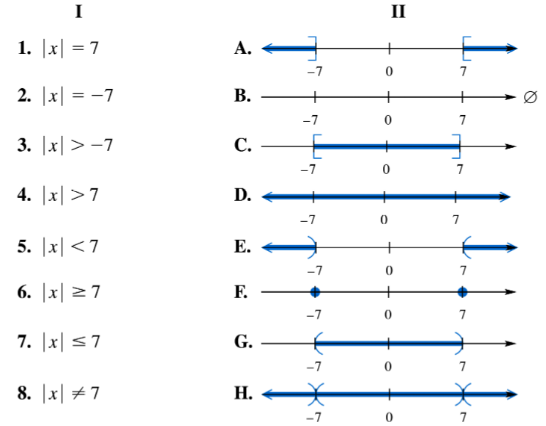
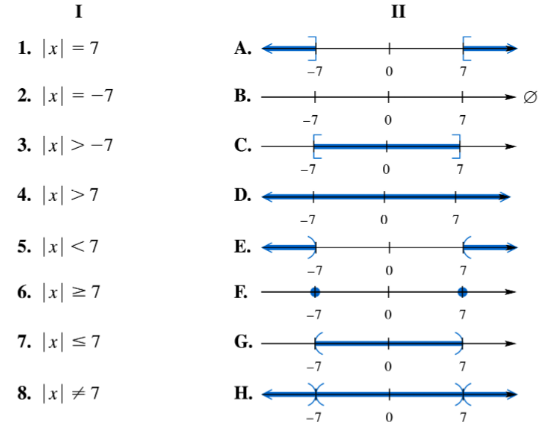
Match each equation or inequality in Column I with the graph of its solution set in Column II. | x | = 7
Problem 1
Match the equation in Column I with its solution(s) in Column II. x2 = 25
Problem 1
Solve each problem. How long will it take a car to travel 400 mi at an average rate of 50 mph?
Problem 1
Solve each equation. 2x+8 = 3x+2
Problem 2
Match the equation in Column I with its solution(s) in Column II. x2 = -25
Problem 2
Match the inequality in each exercise in Column I with its equivalent interval notation in Column II. x≤6
Problem 2
Match each equation or inequality in Column I with the graph of its solution set in Column II. | x | = -7
Problem 2
Solve each problem. If a train travels at 80 mph for 15 min, what is the distance traveled?
Problem 3
Match the inequality in each exercise in Column I with its equivalent interval notation in Column II. -2 < x ≤ 6
Problem 3
Solve each equation. 5x-2(x+4)=3(2x+1)
Problem 3
Match the equation in Column I with its solution(s) in Column II. x2 + 5 = 0
Problem 3
Match each equation or inequality in Column I with the graph of its solution set in Column II. | x | > -7
Problem 3
Solve each problem. If a person invests $500 at 2% simple interest for 4 yr, how much interest is earned?
Problem 3a
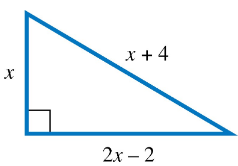
Answer each question. Sides of a Right TriangleTo solve for the lengths of the right triangle sides, which equation is correct?
A. x^2=(2x-2)^2+(x+4)^2 B. x^2+(x+4)^2=(2x-2)^2 C. x^2=(2x-2)^2-(x+4)^2 D. x^2+(2x-2)^2=(x+4)^2
Problem 4
Match each equation or inequality in Column I with the graph of its solution set in Column II. | x | > 7
Problem 4
Match the equation in Column I with its solution(s) in Column II. x2 - 5 = 0
Problem 4
Match the inequality in each exercise in Column I with its equivalent interval notation in Column II. x2≥0
Problem 5
Match the inequality in each exercise in Column I with its equivalent interval notation in Column II . x≥-6
Problem 5
Match each equation or inequality in Column I with the graph of its solution set in Column II. | x | < 7
Problem 5
Solve each problem. If 120 L of an acid solution is 75% acid, how much pure acid is there in the mixture?
Problem 5
Solve each equation. A= 24f / B(p+1), for f (approximate annual interest rate)
Problem 6
Match each equation or inequality in Column I with the graph of its solution set in Column II. | x | ≥ 7
Problem 6
Decide whether each statement is true or false. The solution set of 2x+5=x -3 is {-8}.
Problem 6
Match the inequality in each exercise in Column I with its equivalent interval notation in Column II. 6≤x
Problem 6a
Decide whether each statement is true or false. If false, correct the right side of the equation. √-25 = 5i
Problem 7
Solve each problem. Suppose two acid solutions are mixed. One is 26% acid and the other is 34% acid. Which one of the following concentrations cannot possibly be the concentration of the mixture? A. 24% B. 30% C. 31% D. 33%
Problem 7
Solve each problem. If x represents the number of pennies in a jar in an applied problem, which of the following equations cannot be a correct equation for finding x? (Hint:Solve the equations and consider the solutions.)
A. 5x+3 =11
B.12x+6 =-4
C.100x =50(x+3)
D. 6(x+4) =x+24
Problem 7
Match each equation or inequality in Column I with the graph of its solution set in Column II. | x | ≤ 7
Problem 7
Match each equation in Column I with the correct first step for solving it in Column II. √(x+5) = 7