Back
BackProblem 90
Begin by graphing the absolute value function, f(x) = |x|. Then use transformations of this graph to graph the given function. g(x) = -|x + 4| +2
Problem 90a
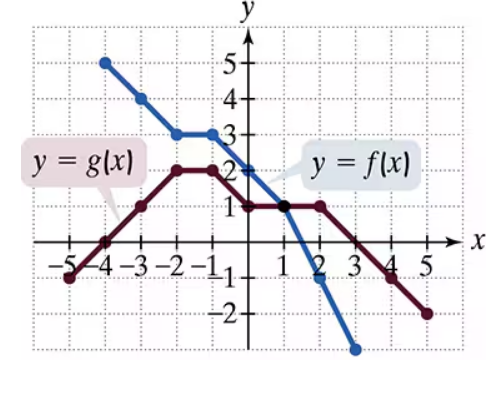
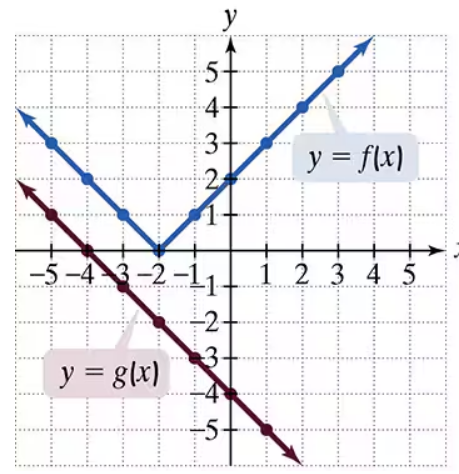
Use the graphs of f and g to solve Exercises 83–90.
Graph f-g.
Problem 91
Use the graphs of f and g to evaluate each composite function.
(fog) (-1)
Problem 91
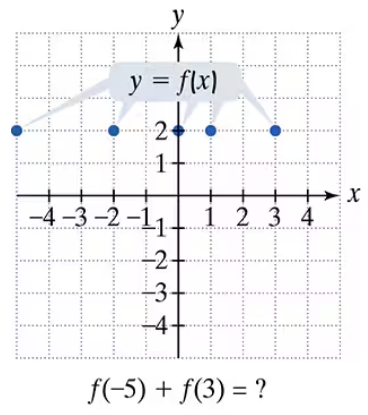
In Exercises 77–92, use the graph to determine a. the function's domain; b. the function's range; c. the x-intercepts, if any; d. the y-intercept, if any; and e. the missing function values, indicated by question marks, below each graph.
Problem 92
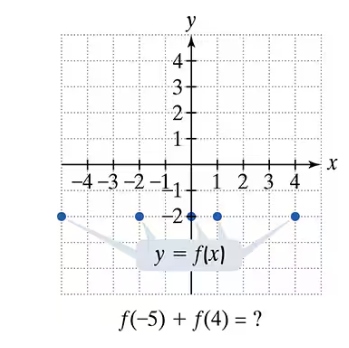
In Exercises 77–92, use the graph to determine a. the function's domain; b. the function's range; c. the x-intercepts, if any; d. the y-intercept, if any; and e. the missing function values, indicated by question marks, below each graph.
Problem 92
Begin by graphing the absolute value function, f(x) = |x|. Then use transformations of this graph to graph the given function. h(x) = 2|x+3|
Problem 93
The functions in Exercises 93–95 are all one-to-one. For each function, (a) find an equation for f-1(x), the inverse function. (b) Verify that your equation is correct by showing that f(f-1(x)) = x and f-1(f(x)) = x. f(x) = 4x - 3
Problem 93
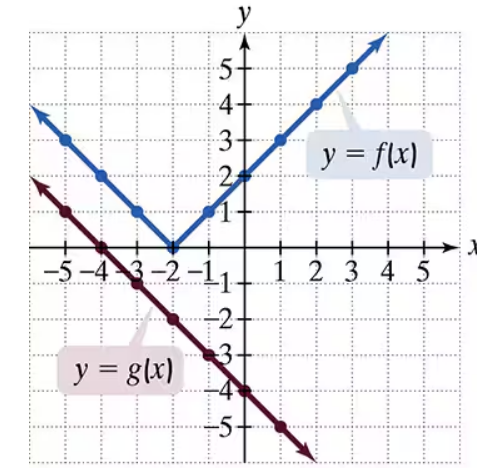
Let f(x) = x² − x + 4 and g(x) = 3x – 5. Find g (1) and f(g(1)).
Problem 93
Use the graphs of f and g to evaluate each composite function.
(go f) (0)
Problem 94
Begin by graphing the absolute value function, f(x) = |x|. Then use transformations of this graph to graph the given function. g(x) = -2|x+3|+2
Problem 94a
Let f(x) = x² − x + 4 and g(x) = 3x – 5. Find g(-1) and f(g(-1)).
Problem 95
Let f and g be defined by the following table: Find
Problem 95
Determine whether each statement is true or false. If the statement is false, make the necessary change(s) to produce a true statement.
If and , find and .
Problem 95
The functions in Exercises 93–95 are all one-to-one. For each function, (a) find an equation for f^(-1)x, the inverse function. (b) Verify that your equation is correct by showing that f(f^(-1)(x)) = x and f^(-1)(f(x)) = x. f(x) = (x - 7)/(x + 2)
Problem 95
Find all values of x satisfying the given conditions. f(x) = 2x − 5, g(x) = x² − 3x + 8, and (ƒ o g) (x) = 7.
Problem 95a
Begin by graphing the standard cubic function, f(x) = x³. Then use transformations of this graph to graph the given function. g(x) = x³-3
Problem 96
In Exercises 95–96, let f and g be defined by the following table: Find |ƒ(1) − f(0)| − [g (1)]² +g(1) ÷ ƒ(−1) · g (2) .
Problem 97
Begin by graphing the standard cubic function, f(x) = x3. Then use transformations of this graph to graph the given function. g(x) = (x − 3)3
Problem 98
Which graphs in Exercises 96–99 represent functions that have inverse functions?
Problem 99
Begin by graphing the standard cubic function, f(x) = x³. Then use transformations of this graph to graph the given function. h(x) = -x³
Problem 100
Solve by completing the square: 2x² – 5x + 1 = 0.
Problem 101
Begin by graphing the standard cubic function, f(x) = x³. Then use transformations of this graph to graph the given function. h(x) = x³/2
Problem 101
In Exercises 101–102, find an equation for f^(-1)(x). Then graph f and f^(-1) in the same rectangular coordinate system. f(x) = 1 - x^2, x ≥ 0.
Problem 101
Solve: 5x3/4- 15 = 0.
Problem 102
Solve and graph the solution set on a number line: 3|2x-1| ≥ 21
Problem 103
Exercises 103–105 will help you prepare for the material covered in the next section. Let (x1, y₁) = (7, 2) and (x2, y2) = (1, −1). Find √[(x2 − x1)² + (y2 − y₁)²]. Express the - answer in simplified radical form.
Problem 104
Exercises 103–105 will help you prepare for the material covered in the next section. Use a rectangular coordinate system to graph the circle with center (1, -1) and radius 1.
Problem 104
Begin by graphing the standard cubic function, f(x) = x³. Then use transformations of this graph to graph the given function. r(x) = (x − 2)³ +1
Problem 105
In Exercises 105–106, find the midpoint of each line segment with the given endpoints. (2, 6) and (-12, 4)
Problem 105
Exercises 103–105 will help you prepare for the material covered in the next section. Solve by completing the square: y² – 6y — 4 = 0.