 Back
BackProblem 73
In Exercises 61–76, solve each absolute value equation or indicate that the equation has no solution. |x + 1| + 5 = 3
Problem 73a
Solve each equation in Exercises 65–74 using the quadratic formula. x2 - 6x + 10 = 0
Problem 74
In Exercises 71–78, solve each equation. Then determine whether the equation is an identity, a conditional equation, or an inconsistent equation. 4(x + 5) = 21 + 4x
Problem 74
Exercises 73–75 will help you prepare for the material covered in the next section. Simplify: √18 - √8
Problem 74a
Determine whether each statement is true or false. If the statement is false, make the necessary change(s) to produce a true statement. The ordered pair (2, 5) satisfies 3y - 2x = - 4.
Problem 75
In Exercises 71–78, solve each equation. Then determine whether the equation is an identity, a conditional equation, or an inconsistent equation. 10x + 3 = 8x + 3
Problem 75
In Exercises 75–82, compute the discriminant. Then determine the number and type of solutions for the given equation.
Problem 75
In Exercises 59–94, solve each absolute value inequality. |(2x + 2)/4| ≥ 2
Problem 75
In Exercises 61–76, solve each absolute value equation or indicate that the equation has no solution. |2x - 1| + 3 = 3
Problem 75
Solve each equation by the method of your choice.
Problem 75a
Exercises 73–75 will help you prepare for the material covered in the next section. Rationalize the denominator: (7 + 4√2)/(2 - 5√2).
Problem 76a
In Exercises 71–78, solve each equation. Then determine whether the equation is an identity, a conditional equation, or an inconsistent equation. 5x + 7 = 2x + 7
Problem 77
Solve each equation by the method of your choice.
Problem 77
In Exercises 59–94, solve each absolute value inequality. |3 - (2/3)x| > 5
Problem 77
The rule for rewriting an absolute value equation without absolute value bars can be extended to equations with two sets of absolute value bars: If u and v represent algebraic expressions, then |u| = |v| is equivalent to u = v or u = - v. Use this to solve the equations in Exercises 77–84. |3x - 1| = |x + 5|
Problem 77
In Exercises 75–82, compute the discriminant. Then determine the number and type of solutions for the given equation.
Problem 77a
List the quadrant or quadrants satisfying each condition. x3 > 0 and y3 <0
Problem 79
In Exercises 59–94, solve each absolute value inequality. 3|x - 1| + 2 ≥ 8
Problem 79
The rule for rewriting an absolute value equation without absolute value bars can be extended to equations with two sets of absolute value bars: If u and v represent algebraic expressions, then |u| = |v| is equivalent to u = v or u = - v. Use this to solve the equations in Exercises 77–84. |4x - 3| = |4x - 5|
Problem 79a
Compute the discriminant. Then determine the number and type of solutions for the given equation. x2 - 2x + 1 = 0
- In Exercises 77–92, use the graph to determine a. the function's domain; b.the x-intercepts, if any; and e. the missing function values, indicated by question marks, below each graph.
Problem 80
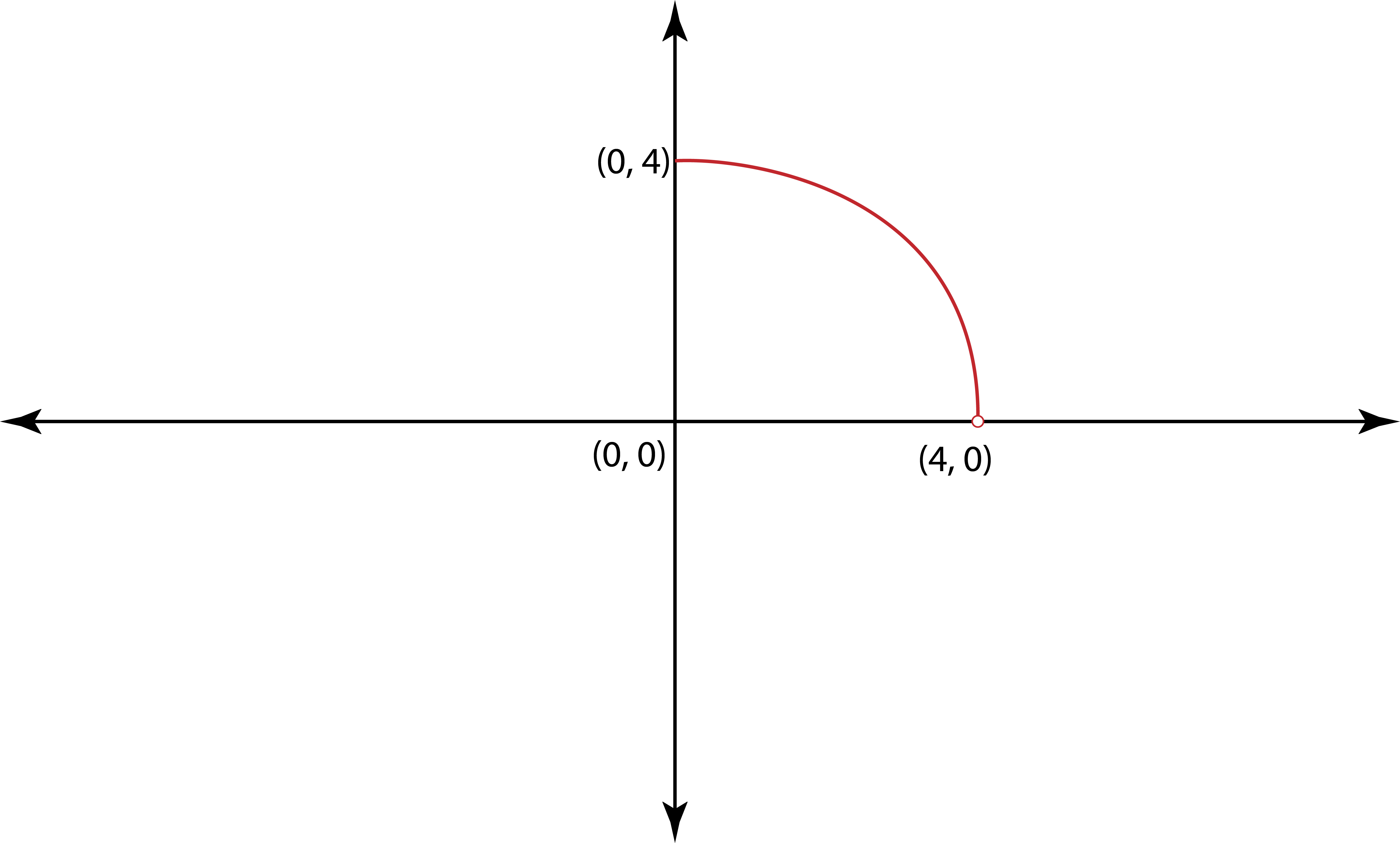
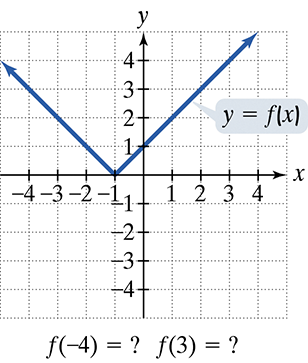
Problem 80a
Solve each absolute value inequality. 5|2x + 1| - 3 ≥ 9
Problem 81
The rule for rewriting an absolute value equation without absolute value bars can be extended to equations with two sets of absolute value bars: If u and v represent algebraic expressions, then |u| = |v| is equivalent to u = v or u = - v. Use this to solve the equations in Exercises 77–84.
Problem 81
In Exercises 59–94, solve each absolute value inequality. - 2|x - 4| ≥ - 4
Problem 81a
Compute the discriminant. Then determine the number and type of solutions for the given equation. x2 - 3x - 7 = 0
Problem 83
The rule for rewriting an absolute value equation without absolute value bars can be extended to equations with two sets of absolute value bars: If u and v represent algebraic expressions, then |u| = |v| is equivalent to u = v or u = - v. Use this to solve the equations in Exercises 77–84.
Problem 83
Solve each equation in Exercises 83–108 by the method of your choice. 2x2 - x = 1
Problem 83a
Solve each absolute value inequality. - 4|1 - x| < - 16
Problem 85
In Exercises 59–94, solve each absolute value inequality. 3 ≤ |2x - 1|
Problem 85
Solve each equation in Exercises 83–108 by the method of your choice.
