The equations in Exercises 79–90 combine the types of equations we have discussed in this section. Solve each equation. Then state whether the equation is an identity, a conditional equation, or an inconsistent equation. 2/x + 1/2 = 3/4

Solve each polynomial equation in Exercises 86–87. 2x^4 = 50 x^2

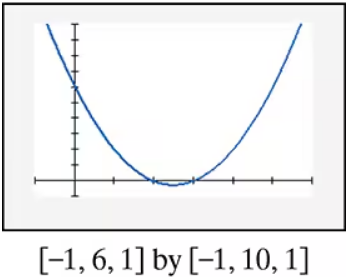
In Exercises 85–90, find the x-intercepts of the graph of each equation. Then use the x-intercepts to match the equation with its graph. [The graphs are labeled (a) through (f).]

a)b)c)d)e)f)

$y = \sqrt{x - 4} + \sqrt{x + 4} - 4$

In Exercises 59–94, solve each absolute value inequality. 5 > |4 - x|

Solve each equation in Exercises 83–108 by the method of your choice. $3x^2=60$

The equations in Exercises 79–90 combine the types of equations we have discussed in this section. Solve each equation. Then state whether the equation is an identity, a conditional equation, or an inconsistent equation. 4/(x - 2) + 3/(x + 5) = 7/(x + 5)(x - 2)

Solve each radical equation in Exercises 88–89. √ (2x-3) + x = 3

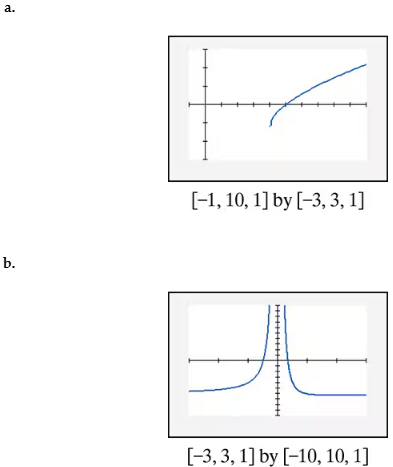
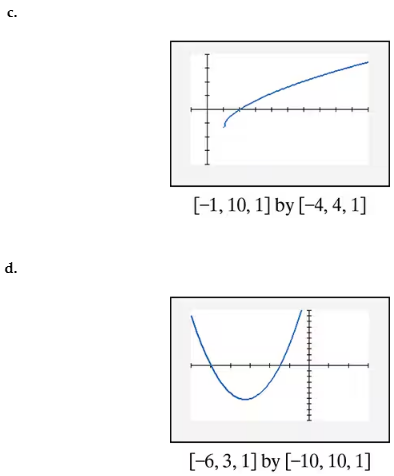
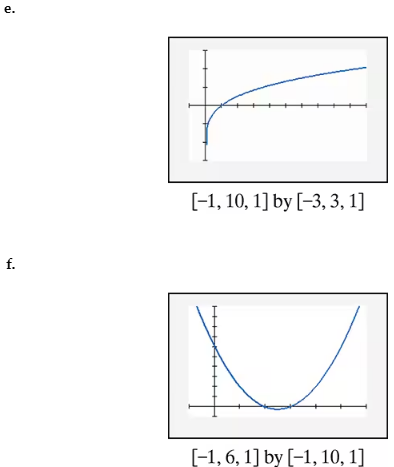
In Exercises 85–90, find the x-intercepts of the graph of each equation. Then use the x-intercepts to match the equation with its graph. [The graphs are labeled (a) through (f).]

<Image>

$y = x^{-2} - x^{-1} - 6$

In Exercises 59–94, solve each absolute value inequality. 1 < |2 - 3x|

Solve each equation in Exercises 83–108 by the method of your choice. $x^2-2x=1$

The equations in Exercises 79–90 combine the types of equations we have discussed in this section. Solve each equation. Then state whether the equation is an identity, a conditional equation, or an inconsistent equation. 4x/(x + 3) - 12/(x - 3) = (4x² + 36)/(x² - 9)

In Exercises 85–90, find the x-intercepts of the graph of each equation. Then use the x-intercepts to match the equation with its graph. [The graphs are labeled (a) through (f).] y = 2(x + 2)^2 + 5(x + 2) - 3

The equations in Exercises 79–90 combine the types of equations we have discussed in this section. Solve each equation. Then state whether the equation is an identity, a conditional equation, or an inconsistent equation. 4/(x² + 3x - 10) - 1/(x² + x - 6) = 3/(x² - x - 12)

In Exercises 59–94, solve each absolute value inequality. $12 < \left| -2x + \frac{6}{7} \right| + \frac{3}{7}$

Solve each equation in Exercises 83–108 by the method of your choice. (2x + 3)(x + 4) = 1

Solve each equation in Exercises 92–93 by making an appropriate substitution. x^4 - 5x^2 + 4 = 0

In Exercises 91–100, find all values of x satisfying the given conditions. y = |2 - 3x| and y = 13

Solve each equation in Exercises 83–108 by the method of your choice. (2x - 5)(x + 1) = 2

Solve each equation in Exercises 83–108 by the method of your choice. (3x - 4)² = 16

Solve each absolute value inequality. 4 + |3 - x/3| ≥ 9

Solve the equations containing absolute value in Exercises 94–95. |2x+1| = 7

In Exercises 91–100, find all values of x satisfying the given conditions. $y = x - \sqrt{x - 2} \quad \text{and} \quad y = 4$

In Exercises 95–102, use interval notation to represent all values of x satisfying the given conditions. $y_1 = \frac{x}{2} + 3, \quad y_2 = \frac{x}{3} + \frac{5}{2}, \quad \text{and} \quad y_1 \leq y_2$

In Exercises 95–99, perform the indicated operations and write the result in standard form. 4/(2 + i)(3 - i)

Solve each equation in Exercises 83–108 by the method of your choice. $3x^2-12x+12=0$

Evaluate x² - x for the value of x satisfying 4(x - 2) + 2 = 4x - 2(2 - x).

In Exercises 91–100, find all values of x satisfying the given conditions. $y=x^3+4x^2-x+6$ and $y=10$

Solve each equation in Exercises 83–108 by the method of your choice. $9-6x+x^2=0$

Perform the indicated operations and write the result in standard form. (1 + i)/(1 + 2i) + (1 - i)/(1 - 2i)

Use interval notation to represent all values of x satisfying the given conditions. y₁ = (2/3)(6x - 9) + 4, y₂ = 5x + 1, and y₁ > y₂