Finding g on a small airless planet Explorers on a small airless planet used a spring gun to launch a ball bearing vertically upward from the surface at a launch velocity of 15 m/sec. Because the acceleration of gravity at the planet’s surface was gₛ m/sec², the explorers expected the ball bearing to reach a height of s = 15t − (1/2)gₛt² m t sec later. The ball bearing reached its maximum height 20 sec after being launched. What was the value of gₛ?
Table of contents
- 0. Functions7h 54m
- Introduction to Functions16m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms36m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
- 8. Definite Integrals4h 44m
- 9. Graphical Applications of Integrals2h 27m
- 10. Physics Applications of Integrals 3h 16m
- 11. Integrals of Inverse, Exponential, & Logarithmic Functions2h 31m
- 12. Techniques of Integration7h 41m
- 13. Intro to Differential Equations2h 55m
- 14. Sequences & Series5h 36m
- 15. Power Series2h 19m
- 16. Parametric Equations & Polar Coordinates7h 58m
4. Applications of Derivatives
Motion Analysis
Problem 3.4.15a
Textbook Question
The accompanying figure shows the velocity v = ds/dt = f(t) (m/sec) of a body moving along a coordinate line.
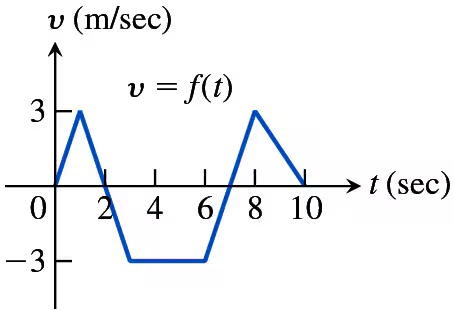
a. When does the body reverse direction?
 Verified step by step guidance
Verified step by step guidance1
To determine when the body reverses direction, we need to find when the velocity changes sign. This occurs when the velocity function v(t) crosses the horizontal axis (v = 0).
Examine the graph of v(t) to identify the points where the curve crosses the t-axis. These points are where the velocity is zero.
From the graph, observe that the velocity crosses the t-axis at approximately t = 2 seconds, t = 6 seconds, and t = 9 seconds.
At these points, the velocity changes from positive to negative or from negative to positive, indicating a reversal in direction.
Thus, the body reverses direction at t = 2 seconds, t = 6 seconds, and t = 9 seconds.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
2mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Velocity and Direction
Velocity is a vector quantity that indicates the rate of change of position with respect to time. When analyzing motion, the sign of the velocity determines the direction of movement. A positive velocity indicates motion in one direction, while a negative velocity indicates motion in the opposite direction. Understanding how velocity changes over time is crucial for determining when an object reverses its direction.
Recommended video:
Derivatives Applied To Velocity
Critical Points and Zeroes
Critical points occur where the velocity function is zero or undefined. These points are essential for analyzing motion because they indicate potential changes in direction. In the context of the graph, when the velocity crosses the time axis (where v = 0), it signifies that the body may be reversing its direction. Identifying these zeroes helps in understanding the overall motion of the object.
Recommended video:

Critical Points
Graph Interpretation
Interpreting graphs is a fundamental skill in calculus, particularly when analyzing functions like velocity. The graph of velocity versus time provides visual insights into how the velocity changes over time. By examining the graph, one can identify intervals of positive and negative velocity, as well as points where the velocity is zero, which are critical for determining when the body reverses direction.
Recommended video:
Graphing The Derivative

 6:29m
6:29mWatch next
Master Derivatives Applied To Velocity with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice
Textbook Question
