Here are the essential concepts you must grasp in order to answer the question correctly.
Cosine Function
The cosine function, denoted as cos(x), is a periodic function that represents the x-coordinate of a point on the unit circle corresponding to an angle x. It oscillates between -1 and 1, with a period of 2π. Understanding its graph is crucial for analyzing the behavior of related functions, such as secant.
Recommended video:
Graph of Sine and Cosine Function
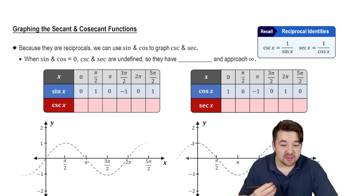
Secant Function
The secant function, denoted as sec(x), is the reciprocal of the cosine function, defined as sec(x) = 1/cos(x). It is undefined wherever cos(x) equals zero, leading to vertical asymptotes in its graph. The behavior of sec(x) is directly influenced by the values of cos(x), particularly its signs.
Recommended video:
Graphs of Secant and Cosecant Functions
Graphing Trigonometric Functions
Graphing trigonometric functions involves plotting their values over a specified interval, which helps visualize their periodic nature and relationships. When graphing y = cos(x) and y = sec(x) together, one can observe how sec(x) behaves in relation to cos(x), particularly noting where sec(x) approaches infinity as cos(x) approaches zero.
Recommended video:
Introduction to Trigonometric Functions
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem:


 5:53m
5:53m