1. Limits and Continuity

Continuity

1. Limits and Continuity

Continuity

Struggling with Business Calculus?

Join thousands of students who trust us to help them ace their exams!Watch the first video

Multiple Choice

Determine the interval(s) for which the function is continuous.

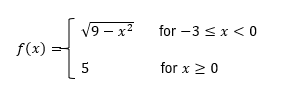
$open bracket negative 3 comma 0 close paren comma open bracket 0 comma infinity close paren$

$(-∞,0),[0,∞)$

$(-∞,∞)$

The function is not continuous anywhere.

Verified step by step guidance

Step 1: Analyze the function piecewise. The function is defined as $ f(x) = \sqrt{9 - x^2} $ for $ -3 \leq x < 0 $, and $ f(x) = 5 $ for $ x \geq 0 $.

Step 2: Check the continuity of $ \sqrt{9 - x^2} $ on the interval $ -3 \leq x < 0 $. The square root function is continuous as long as the argument inside the square root is non-negative. Here, $ 9 - x^2 \geq 0 $ is satisfied for $ -3 \leq x \leq 3 $, so $ \sqrt{9 - x^2} $ is continuous on $ -3 \leq x < 0 $.

Step 3: Check the continuity of $ f(x) = 5 $ for $ x \geq 0 $. Since $ f(x) = 5 $ is a constant function, it is continuous for all $ x \geq 0 $.

Step 4: Examine the point $ x = 0 $, where the two pieces of the function meet. For $ x \to 0^- $, $ f(x) \to \sqrt{9 - 0^2} = 3 $. For $ x \to 0^+ $, $ f(x) = 5 $. Since the left-hand limit (3) does not equal the right-hand limit (5), the function is not continuous at $ x = 0 $.

Step 5: Combine the results. The function is continuous on $ [-3, 0) $ and $ [0, \infty) $, but not at $ x = 0 $. Therefore, the intervals of continuity are $ [-3, 0) \cup [0, \infty) $.

5:34m

Watch next

Master Intro to Continuity with a bite sized video explanation from Patrick

Start learning

Continuity practice set

Problem sets built by lead tutors

Expert video explanations

Go to Practice