Find the shaded area between & .
Table of contents
- 0. Functions4h 53m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation2h 18m
- 4. Derivatives of Exponential & Logarithmic Functions1h 16m
- 5. Applications of Derivatives2h 19m
- 6. Graphical Applications of Derivatives6h 0m
- 7. Antiderivatives & Indefinite Integrals48m
- 8. Definite Integrals4h 36m
- 9. Graphical Applications of Integrals1h 43m
- 10. Integrals of Inverse, Exponential, & Logarithmic Functions21m
- 11. Techniques of Integration2h 7m
- 12. Trigonometric Functions6h 54m
- Angles29m
- Trigonometric Functions on Right Triangles1h 8m
- Solving Right Triangles23m
- Trigonometric Functions on the Unit Circle1h 19m
- Graphs of Sine & Cosine46m
- Graphs of Other Trigonometric Functions32m
- Trigonometric Identities52m
- Derivatives of Trig Functions42m
- Integrals of Basic Trig Functions28m
- Integrals of Other Trig Functions10m
- 13: Intro to Differential Equations2h 23m
- 14. Sequences & Series2h 8m
- 15. Power Series2h 19m
- 16. Probability & Calculus45m
9. Graphical Applications of Integrals
Area Between Curves
Struggling with Business Calculus?
Join thousands of students who trust us to help them ace their exams!Watch the first videoMultiple Choice
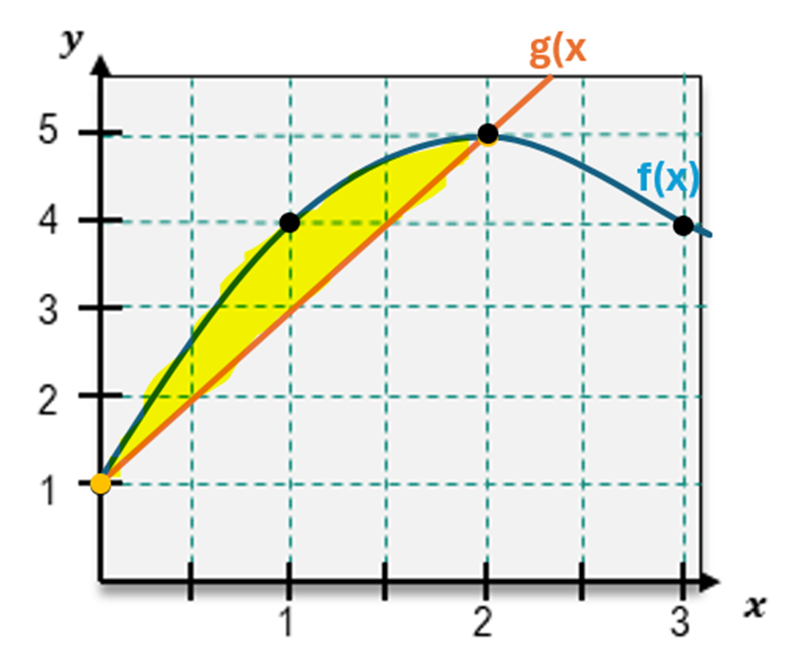
Sketch the region bounded by f(x)=−(x−2)2+5 & g(x)=4x on the interval [0,1]. Then set up an integral to represent the region's area and evaluate.
A
Integral = ∫01(−x2+9)dx; Area: 0.33
B
Integral = ∫01−x2+1dx; Area = 0.67
C
Integral = ;∫04(−x2+9)dx Area: 21.33
D
Integral = ∫01−x2+1dx; Area = 22.67
 Verified step by step guidance
Verified step by step guidance1
Step 1: Identify the functions and the interval. The functions are f(x) = -(x-2)^2 + 5 (a downward-opening parabola) and g(x) = 4x (a straight line). The interval is [0,1].
Step 2: Sketch the graphs of f(x) and g(x) on the interval [0,1]. The parabola f(x) peaks at x = 2 and has a vertex at (2,5). The line g(x) starts at (0,0) and increases linearly. The region of interest is the area between these two curves within the interval [0,1].
Step 3: Determine the integral setup for the area. The area between two curves is calculated as the integral of the upper function minus the lower function over the given interval. Here, g(x) is below f(x) on [0,1], so the integral is ∫[0,1] (f(x) - g(x)) dx.
Step 4: Substitute the expressions for f(x) and g(x) into the integral. This gives ∫[0,1] [-(x-2)^2 + 5 - 4x] dx.
Step 5: Simplify the integrand and prepare for evaluation. Expand -(x-2)^2 to get -x^2 + 4x - 4. Combine terms to simplify the integrand to -x^2 + 9 - 4x. The integral becomes ∫[0,1] (-x^2 + 9 - 4x) dx. Evaluate this integral to find the area.

 5:23m
5:23mWatch next
Master Finding Area Between Curves on a Given Interval with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice
Multiple Choice
Area Between Curves practice set



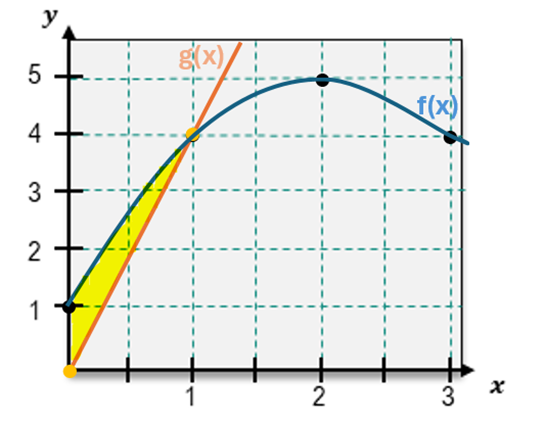
![Graph showing the area between two curves, f(x) in blue and g(x) in orange, highlighted in yellow on the interval [0,1].](https://static.studychannel-dev.pearsondev.tech/courses/calculus/thumbnails/eddf84c8-d1bf-4f07-899c-39929d63ad4b)