Multiple Choice
Find the area of the shaded region shown in the first quadrant between &
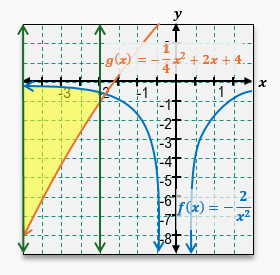
8.17
4.17
-12.17
0.50
 Verified step by step guidance
Verified step by step guidance
 5:23m
5:23mMaster Finding Area Between Curves on a Given Interval with a bite sized video explanation from Patrick
Start learning
