Back
BackProblem 1a
The electrons in a rigid box emit photons of wavelength 1484 nm during the 3→2 transition. What kind of photons are they—infrared, visible, or ultraviolet?
Problem 1b
The electrons in a rigid box emit photons of wavelength 1484 nm during the 3→2 transition. How long is the box in which the electrons are confined?
Problem 6
A 16-nm-long box has a thin partition that divides the box into a 4-nm-long section and a 12-nm-long section. An electron confined in the shorter section is in the n = 2 state. The partition is briefly withdrawn, then reinserted, leaving the electron in the longer section of the box. What is the electron’s quantum state after the partition is back in place?
Problem 9
A finite potential well has depth U₀ = 2.00 eV. What is the penetration distance for an electron with energy (a) 0.50 eV, (b) 1.00 eV, and (c) 1.50 eV?
Problem 11
A helium atom is in a finite potential well. The atom’s energy is 1.0 eV below U₀. What is the atom’s penetration distance into the classically forbidden region?
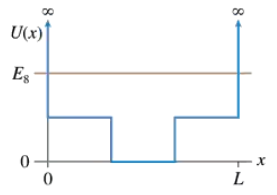
Problem 13
Sketch the n = 8 wave function for the potential energy shown in FIGURE EX40.13.
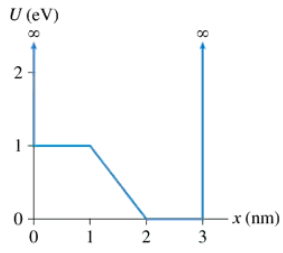
Problem 15a
The graph in FIGURE EX40.15 shows the potential-energy function U(x) of a particle. Solution of the Schrödinger equation finds that the n = 3 level has E3 = 0.5 eV and that the n = 6 level has E6 = 2.0 eV. Redraw this figure and add to it the energy lines for the n = 3 and n = 6 states.
Problem 17a
INT An electron is confined in a harmonic potential well that has a spring constant of 2.0 N/m. What are the first three energy levels of the electron?
Problem 17b
INT An electron is confined in a harmonic potential well that has a spring constant of 2.0 N/m. What wavelength photon is emitted if the electron undergoes a 3→1 quantum jump?
Problem 21
INT An electron is confined in a harmonic potential well that has a spring constant of 12.0 N/m. What is the longest wavelength of light that the electron can absorb?
Problem 22
Use the data from Figure 40.24 to calculate the first three vibrational energy levels of a C=O carbon-oxygen double bond.
Problem 24
An electron approaches a 1.0-nm-wide potential-energy barrier of height 5.0 eV. What energy electron has a tunneling probability of (a) 10%, (b) 1.0%, and (c) 0.10%?
Problem 26
CALC Suppose that ψ1(x) and ψ2(x) are both solutions to the Schrödinger equation for the same potential energy U(x). Prove that the superposition ψ(x)=Aψ1(x) + Bψ2(x) is also a solution to the Schrödinger equation.
Problem 27a
A 2.0-μm-diameter water droplet is moving with a speed of 1.0 μm/s in a 20-μm-long box. Estimate the particle’s quantum number.
Problem 29a
INT Model an atom as an electron in a rigid box of length 0.100 nm, roughly twice the Bohr radius. What are the four lowest energy levels of the electron?
Problem 29b
INT Model an atom as an electron in a rigid box of length 0.100 nm, roughly twice the Bohr radius. Calculate all the wavelengths that would be seen in the emission spectrum of this atom due to quantum jumps between these four energy levels. Give each wavelength a label λn→m to indicate the transition.
Problem 32a
A particle confined in a rigid one-dimensional box of length 10 fm has an energy level En = 32.9 MeV and an adjacent energy level En+1 = 51.4 MeV. Determine the values of n and n+1.
Problem 32b
A particle confined in a rigid one-dimensional box of length 10 fm has an energy level En = 32.9 MeV and an adjacent energy level En+1 = 51.4 MeV. Draw an energy-level diagram showing all energy levels from 1 through n+1. Label each level and write the energy beside it.
Problem 32c
A particle confined in a rigid one-dimensional box of length 10 fm has an energy level En = 32.9 MeV and an adjacent energy level En+1 = 51.4 MeV. Sketch the n+1 wave function on the n+1 energy level.
Problem 32e
A particle confined in a rigid one-dimensional box of length 10 fm has an energy level En = 32.9 MeV and an adjacent energy level En+1 = 51.4 MeV. What is the mass of the particle? Can you identify it?
Problem 33b
CALC Consider a particle in a rigid box of length L. For each of the states n = 1, n = 2, and n = 3: Where, in terms of L, are the positions at which the particle is most likely to be found?
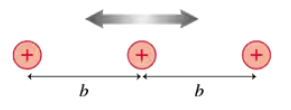
Problem 34b
In most metals, the atomic ions form a regular arrangement called a crystal lattice. The conduction electrons in the sea of electrons move through this lattice. FIGURE P40.34 is a one-dimensional model of a crystal lattice. The ions have mass m, charge e, and an equilibrium separation b. Suppose this crystal consists of aluminum ions with an equilibrium spacing of 0.30 nm. What are the energies of the four lowest vibrational states of these ions?
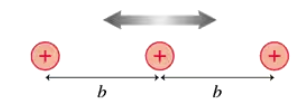
Problem 34c
In most metals, the atomic ions form a regular arrangement called a crystal lattice. The conduction electrons in the sea of electrons move through this lattice. FIGURE P40.34 is a one-dimensional model of a crystal lattice. The ions have mass m, charge e, and an equilibrium separation b. What wavelength photons are emitted during quantum jumps between adjacent energy levels? Is this wavelength in the infrared, visible, or ultraviolet portion of the spectrum?
Problem 36
For a particle in a finite potential well of width L and depth U0, what is the ratio of the probability Prob(in δx at x=L+η) to the probability Prob(in δx at x = L)?
Problem 37a
A typical electron in a piece of metallic sodium has energy −E₀ compared to a free electron, where E₀ is the 2.36 eV work function of sodium. At what distance beyond the surface of the metal is the electron’s probability density 10% of its value at the surface?
Problem 39a
CALC Determine the normalization constant A1 for the n = 1 ground-state wave function of the quantum harmonic oscillator. Your answer will be in terms of b.
Problem 42a
CALC A particle of mass m has the wave function ψ(x) = Ax exp (−x²/a²) when it is in an allowed energy level with E = 0. Draw a graph of ψ(x) versus x.
Problem 42b
CALC A particle of mass m has the wave function ψ(x) = Ax exp (−x²/a²) when it is in an allowed energy level with E = 0. At what value or values of x is the particle most likely to be found?
Problem 42c
CALC A particle of mass m has the wave function ψ(x) = Ax exp (−x²/a²) when it is in an allowed energy level with E = 0. Find and graph the potential-energy function U(x).
Problem 43
Figure 40.17 showed that a typical nuclear radius is 4.0 fm. As you’ll learn in Chapter 42, a typical energy of a neutron bound inside the nuclear potential well is En = −20 MeV. To find out how “fuzzy” the edge of the nucleus is, what is the neutron’s penetration distance into the classically forbidden region as a fraction of the nuclear radius?