Back
BackProblem 2
Monochromatic light falls on a slit that is 2.60 x 10⁻³ mm wide. If the angle between the first dark fringes on either side of the central maximum is 29.0° (dark fringe to dark fringe), what is the wavelength of the light used?
Problem 4
Light of wavelength 580 nm falls on a slit that is 3.50 x 10⁻³ mm wide. Estimate how far the first brightest diffraction fringe is from the strong central maximum if the screen is 10.0 m away.
Problem 6
Monochromatic light of wavelength 633 nm falls on a slit. If the angle between the first bright fringes on either side of the central maximum is 32°, estimate the slit width.
Problem 14
(a) Explain why the secondary maxima in the single-slit diffraction pattern do not occur precisely at β/2 = (m + 1/2)π where m = 1, 2, 3, ... .
(b) By differentiating Eq. 35–7 with respect to β show that the secondary maxima occur when β/2 satisfies the relation tan(β/2) = β/2.
(c) Carefully and precisely plot the curves y = β/2 and y = tan β/2. From their intersections, determine the values of β for the first and second secondary maxima. What is the percent difference from β/2 = (m + 1/2)π?
Problem 14c
Explain why the secondary maxima in the single-slit diffraction pattern do not occur precisely at β/2 = (m + 1/2)π where m = 1, 2, 3, ... Carefully and precisely plot the curves y = β/2 and y = tan β/2. From their intersections, determine the values of β for the first and second secondary maxima. What is the percent difference from β/2 = (m + 1/2)π?
Problem 18
Two 0.010-mm-wide slits are 0.030 mm apart (center to center). Determine (a) the spacing between interference fringes for 520-nm light on a screen 1.0 m away and (b) the distance between the two diffraction minima on either side of the central maximum of the envelope.
Problem 20
In a double-slit experiment, let d = 5.00D = 40.0λ. Compare (as a ratio) the intensity of the third-order interference maximum with that of the zero-order maximum.
Problem 22
(a) Derive an expression for the intensity in the interference pattern for three equally spaced slits. Express in terms of δ = 2πd sin θ / λ where d is the distance between adjacent slits and assume the slit width D ≈ λ.
(b) Show that there is only one secondary maximum between principal peaks.
Problem 22b
(III) Derive an expression for the intensity in the interference pattern for three equally spaced slits. Express in terms of δ = 2πd sin θ / λ where d is the distance between adjacent slits and assume the slit width D ≈ λ . Show that there is only one secondary maximum between principal peaks.
Problem 26
The nearest neighboring star to the Sun is about 4 light-years away. If a planet happened to be orbiting this star at an orbital radius equal to that of the Earth–Sun distance, what minimum diameter would an Earth-based telescope’s aperture have to be in order to obtain an image that resolved this star–planet system? Assume the light emitted by the star and planet has a wavelength of 550 nm.
Problem 32
When driving at night, your eyes’ pupils have dilated to a 7.5-mm diameter. If your vision is diffraction limited, what would be the greatest distance at which you could resolve the two headlights of an oncoming car, which are spaced 1.5 m apart? Assume a wavelength of 550 nm for the light.
Problem 35
A 3800-slit/cm grating produces a third-order fringe at a 35.0° angle. What wavelength of light is being used?
Problem 39
A diffraction grating has 6.5 x 10⁵ slits/m. Find the angular spread in the second-order spectrum between red light of wavelength 7.0 x 10⁻⁷ m and blue light of wavelength 4.5 x 10⁻⁷ m.
Problem 41
Show that the second- and third-order spectra of white light produced by a diffraction grating always overlap. What wavelengths overlap?
Problem 43
Suppose the angles measured in Problem 42 were produced when the spectrometer (but not the source) was submerged in water. What then would be the wavelengths (in air)?
Problem 45
Red laser light from a He–Ne laser (λ = 632.8 nm) creates a second-order fringe at 53.2° after passing through a grating. What is the wavelength λ of light that creates a first-order fringe at 21.2°?
Problem 47a
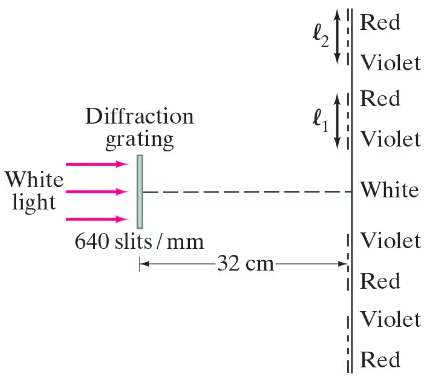
(II) White light passes through a 640-slit/ mm diffraction grating. First-order and second-order visible spectra (“rainbows”) appear on the wall 32 cm away as shown in Fig. 35–40. Determine the widths ℓ₁ and ℓ₂ of the two “rainbows” (400 nm to 700 nm). In which order is the “rainbow” dispersed over a larger distance?
Problem 51
A diffraction grating has 15,000 rulings in its 1.9 cm width. Determine (a) its resolving power in first and second orders, and (b) the minimum wavelength resolution (∆λ) it can yield for λ = 410 nm.
Problem 53
(II) X-rays of wavelength 0.138 nm fall on a crystal whose atoms, lying in planes, are spaced 0.315 nm apart. At what angle Φ (relative to the surface, Fig. 35–28) must the X-rays be directed if the first diffraction maximum is to be observed?
Problem 56
(II) (a) Suppose for a conventional X-ray image that the X-ray beam consists of parallel rays. What would be the magnification of the image? (b) Suppose, instead, that the X-rays come from a point source (as in Fig. 35–31) that is 15 cm in front of a human body which is 25 cm thick, and the film is pressed against the person’s back. Determine and discuss the range of magnifications that result.
<IMAGE>
Problem 68
You want to design a spy satellite to photograph license plate numbers. Assuming it is necessary to resolve points separated by 2 cm with 550-nm light, and that the satellite orbits at a height of 130 km, what minimum lens aperture (diameter) is required?
Problem 69
What is the highest spectral order that can be seen if a grating with 6800 slits per cm is illuminated with 633-nm laser light? Assume normal incidence.
Problem 76
X-rays of wavelength 0.10 nm fall on a microcrystalline powder sample. The sample is located 15 cm from a photographic sensor. The crystal structure of the sample has an atomic spacing of 0.22 nm. Calculate the radii of the diffraction rings corresponding to first- and second-order scattering. Note in Fig. 35–28 that the X-ray beam is deflected through an angle 2Φ.
Problem 78
A slit of width D = 22 μm is cut through a thin aluminum plate. Light with wavelength λ = 620nm passes through this slit and forms a single-slit diffraction pattern on a screen a distance ℓ = 2.0 m away. Defining x to be the distance between the two first minima on either side of the center in this diffraction pattern ( m = +1 and m = -1), find the change ∆x in this distance when the temperature T of the metal plate is changed by an amount ∆T = 55 C°. [Hint: Since λ ≪ D, the first minima occur at a small angle.]