Monochromatic light falling on two slits 0.018 mm apart produces the fifth-order bright fringe at a 12° angle. What is the wavelength of the light used?

(II) Assume that light of a single color, rather than white light, passes through the two-slit setup described in Example 34–4. If the distance from the central fringe to a first-order fringe is measured to be 2.9 mm on the screen, determine the light’s wavelength (in nm) and color (see Fig. 34–11).

(II) Light of wavelength λ passes through a pair of slits separated by 0.17 mm, forming a double-slit interference pattern on a screen located a distance 35 cm away. Suppose that the image in Fig. 34–9a is an actual-size reproduction of this interference pattern. Use a ruler to measure a pertinent distance on this image; then utilize this measured value to determine λ (nm) .

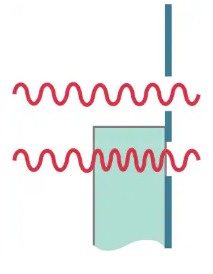
(II) Suppose a thin piece of glass is placed in front of the lower slit in Fig. 34–7 so that the two waves enter the slits 180° out of phase (Fig. 34–44). Describe in detail the interference pattern on the screen.

In a two-slit interference experiment, the path length to a certain point P on the screen differs for one slit in comparison with the other by 1.25λ.

(a) What is the phase difference between the two waves arriving at point P?

(b) Determine the intensity at P, expressed as a fraction of the maximum intensity Iₒ on the screen.

Suppose that one slit of a double-slit apparatus is wider than the other so that the intensity of light passing through it is twice as great. Determine the intensity I as a function of position (θ) on the screen for coherent light.

Consider three equally spaced and equal-intensity coherent sources of light (such as adding a third slit to the two slits of Fig. 34–12). Determine the positions of minima.

(I) If a soap bubble is 120 nm thick, what wavelength is most strongly reflected at the center of the outer surface when illuminated normally by white light? Assume that n = 1.35.

A uniform thin film of alcohol (n = 1.36) lies on a flat glass plate (n = 1.56). When monochromatic light, whose wavelength can be changed, is incident normally, the reflected light is a minimum for λ = 492 nm and a maximum for λ = 615 nm. What is the minimum thickness of the film?

Show that the radius r of the mᵗʰ dark Newton’s ring, as viewed from directly above (Fig. 34–18), is given by r = √mλR where R is the radius of curvature of the curved glass surface and λ is the wavelength of light used. Assume that the thickness of the air gap is much less than R at all points and that r ≪ R . [Hint: Use the binomial expansion.]

(II) When a Newton’s ring apparatus (Fig. 34–18) is immersed in a liquid, the diameter of the tenth dark ring decreases from 2.92 cm to 2.54 cm. What is the refractive index of the liquid? [Hint: See Problem 37.]

A single optical coating reduces reflection to zero for λ = 550 nm. By what factor is the intensity reduced by the coating for λ = 430 nm and λ = 670 nm as compared to no coating? Assume normal incidence.

(II) White light passes through a 640-slit/ mm diffraction grating. First-order and second-order visible spectra (“rainbows”) appear on the wall 32 cm away as shown in Fig. 35–40. Determine the widths ℓ₁ and ℓ₂ of the two “rainbows” (400 nm to 700 nm). In which order is the “rainbow” dispersed over a larger distance?

What is Brewster’s angle for an air-glass (n = 1.56) surface? Specify two answers.

(II) X-rays of wavelength 0.138 nm fall on a crystal whose atoms, lying in planes, are spaced 0.315 nm apart. At what angle Φ (relative to the surface, Fig. 35–28) must the X-rays be directed if the first diffraction maximum is to be observed?

What would Brewster’s angle be for reflections off the surface of water for light coming from beneath the surface? Compare to the angle for total internal reflection, and to Brewster’s angle from above the surface.

Light of wavelength 5.0 x 10⁻⁷ passes through two parallel slits and falls on a screen 5.0 m away. Adjacent bright bands of the interference pattern are 2.0 cm apart.

(a) Find the distance between the slits.

(b) The same two slits are next illuminated by light of a different wavelength, and the fifth minimum for this light occurs at the same point on the screen as the fourth minimum for the previous light. What is the wavelength of the second source of light?

Light of wavelength 690 nm passes through two narrow slits 0.66 mm apart. The screen is 1.75 m away. A second source of unknown wavelength produces its second-order fringe 1.23 mm closer to the central maximum than the 690-nm light. What is the wavelength of the unknown light?

Suppose the mirrors in a Michelson interferometer are perfectly aligned and the path lengths to mirrors M₁ and M₂ are identical. With these initial conditions, an observer sees a bright maximum at the center of the viewing area. Now one of the mirrors is moved a distance x. Determine a formula for the intensity at the center of the viewing area as a function of x, the distance the movable mirror is moved from the initial position.

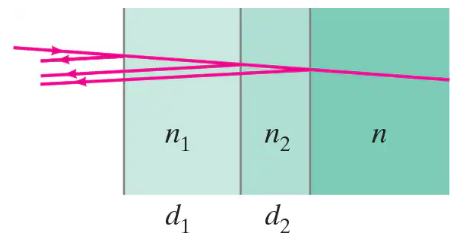
A highly reflective mirror can be made for a particular wavelength at normal incidence by using two thin layers of transparent materials of indices of refraction n₁ and n₂ ( 1 < n₁ < n₂ ) on the surface of the glass (n > n₂). What should be the minimum thicknesses d₁ and d₂ in Fig. 34–49 in terms of the incident wavelength λ, to maximize reflection?

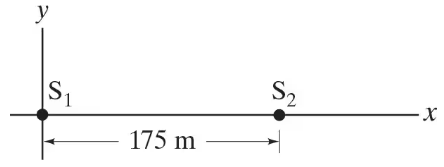
Consider two antennas radiating 6.8-MHz radio waves in phase with each other. They are located at points S₁ and S₂, separated by a distance d = 175 m, Fig. 34–50. Determine the points on the positive y-axis where the signals from the two sources will be out of phase (crests of one meet troughs of the other).

Two narrow slits 0.070 mm apart are illuminated by a very bright 488-nm light source forming an interference pattern on a screen 4.0 m away. Calculate (a) the distance between the m = 0 and m = 1 lines in the pattern and (b) the distance between the m = 100 and m = 101 lines.

Unpolarized light falls on two polarizer sheets whose axes are at right angles. (a) What fraction of the incident light intensity is transmitted? (b) What fraction is transmitted if a third polarizer is placed between the first two so that its axis makes a 58° angle with the axis of the first polarizer? (c) What if the third polarizer is in front of the other two?

Two polarizers are oriented at 55° to each other and plane-polarized light is incident on them. If only 25% of the light gets through both of them, what was the initial polarization direction of the incident light?

At what angle should the axes of two Polaroids be placed so as to reduce the intensity of the incident unpolarized light by an additional factor (after the first Polaroid cuts it in half) of (a) 4, (b) 10, (c) 100?

"Two identical sources S₁ and S₂, separated by distance d, coherently emit light of wavelength λ uniformly in all directions. Defining the x axis with its origin at S₁ as shown in Fig. 34–52, find the locations (expressed as multiples of λ ) where the signals from the two sources are out of phase along this axis for x > 0 , if d = 3λ.

Describe how to rotate the plane of polarization of a plane-polarized beam of light by 90° and produce only a 10% loss in intensity, using polarizers. Let N be the number of polarizers and θ be the (same) angle between successive polarizers.

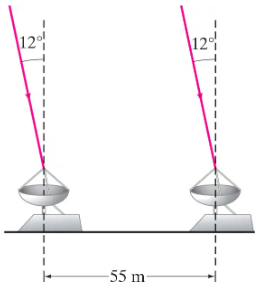
A radio telescope, whose two antennas are separated by 55 m, is designed to receive 3.0-MHz radio waves produced by astronomical objects. The received radio waves create 3.0-MHz electronic signals in the telescope’s left and right antennas. These signals then travel by equal-length cables to a centrally located amplifier, where they are added together. The telescope can be “pointed” to a certain region of the sky by adding the instantaneous signal from the right antenna to a “time-delayed” signal received by the left antenna a time ∆t ago. (This time delay of the left signal can be easily accomplished with the proper electronic circuit.) If a radio astronomer wishes to “view” radio signals arriving from an object oriented at a 12° angle to the vertical as in Fig. 34–54, what time delay ∆t is necessary?