A star is 23.5 light-years from Earth. How long would it take a spacecraft traveling 0.950c to reach that star as measured by observers on the spacecraft?

(II) Suppose that three main-sequence stars could undergo the three changes represented by the three arrows, A, B, and C, in the H–R diagram of Fig. 44–35. For each case, describe the changes in temperature, intrinsic luminosity, and size.

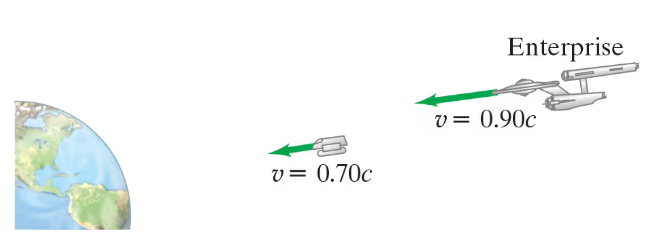
(I) An observer on Earth sees an alien vessel approach at a speed of 0.70c. The fictional starship Enterprise comes to the rescue (Fig. 36–17), overtaking the aliens while moving directly toward Earth at a speed of 0.90c relative to Earth. What is the relative speed of one vessel as seen by the other?

(I) Repeat Problem 19 using the Lorentz transformation and a relative speed v = 1.60 x 10⁸ m/s, but choose the time t to be (a) 3.5μs and (b) 10.0 μs .

Two spaceships leave Earth in opposite directions, each with a speed of 0.50c with respect to Earth.

(a) What is the velocity of spaceship 1 relative to spaceship 2?

(b) What is the velocity of spaceship 2 relative to spaceship 1?

A spaceship traveling at 0.76c away from Earth fires a module with a speed of 0.85c at right angles to its own direction of travel (as seen by the spaceship). What is the speed of the module, and its direction of travel (relative to the spaceship’s direction), seen by an observer on Earth?

A stick of length ℓ₀, at rest in reference frame S, makes an angle θ with the x axis. In reference frame S', which moves to the right with velocity $\overrightarrow{v}$ = vî with respect to S, determine (a) the length l of the stick, and (b) the angle θ it makes with the x' axis.

An observer in reference frame S notes that two events are separated in space by 180 m and in time by 0.80μs. How fast must reference frame S' be moving relative to S in order for an observer in S' to detect the two events as occurring at the same location in space?

In the old West, a marshal riding on a train traveling 35.0 m/s sees a duel between two men standing on the Earth 55.0 m apart parallel to the train. The marshal’s instruments indicate that in his reference frame the two men fired simultaneously.

(a) Which of the two men, the first one the train passes (A) or the second one (B) should be arrested for firing the first shot? That is, in the gunfighter’s frame of reference, who fired first?

(b) How much earlier did he fire?

(c) Who was struck first?

(III) If a particle moves in the xy plane of system S (Fig. 36–12) with speed u in a direction that makes an angle θ with the x axis, show that it makes an angle θ' in S' given by $\tan {\theta }^{\prime }=(\sin \theta )\sqrt{1-v^2/c^2}/(\cos \theta -v/u)$.

Suppose a spacecraft of mass 17,000 kg was accelerated to 0.22c.

(a) How much kinetic energy would it have?

(b) If you used the classical formula for kinetic energy, by what percentage would you be in error?

Make a graph of the kinetic energy versus momentum for (a) a particle of nonzero mass, and (b) a particle with zero mass.

Show that the kinetic energy K of a particle of mass m is related to its momentum p by the equation $p=\frac{\sqrt{K^2+2Km{c}^2}}{c}$.

(III) (a) In reference frame S, a particle has momentum $\overrightarrow{p}=p_{x}i$ along the positive x axis. Show that in frame S’, which moves with speed v as in Fig. 36–12, the momentum has components

$p_x^{\prime }=\frac{px-vE/c^2}{\sqrt{1-v^2/c^2}}$

$p_y^{\prime }=py$

$p_z^{\prime }=pz$

$E^{\prime }=\frac{E-p_{x}v}{\sqrt{1-v^2/c^2}}.$

(These transformation equations hold, actually, for any direction of $\overrightarrow{p}$, as long as the motion of S' is along the x axis.) (b) Show that p_x, p_y, p_z, E/c transform according to the Lorentz transformation in the same way as x, y, z, ct.

A certain galaxy has a Doppler shift given by ƒ₀ - ƒ = 0.1015 ƒ₀. Estimate how fast it is moving away from us.

A spaceship moving toward Earth at 0.65c transmits radio signals at 95.0 MHz. At what frequency should Earth receivers be tuned?

An atomic clock is taken to the North Pole, while another stays at the Equator. How far will they be out of synchronization after 1.5 years has elapsed? [Hint: Use the binomial expansion, Appendix A–2.]

An electron (m = 9.11 x 10⁻³¹ kg) is accelerated from rest to speed v by a conservative force. In this process, its potential energy decreases by 7.20 x 10⁻¹⁴ J . Determine the electron’s speed, v.

A healthy astronaut’s heart rate is 60 beats/min . Flight doctors on Earth can monitor an astronaut’s vital signs remotely while in flight. How fast would an astronaut be flying away from Earth if the doctor measured her heart rate as 52 beats/min?

What minimum amount of electromagnetic energy is needed to produce an electron and a positron together? A positron is a particle with the same mass as an electron, but has the opposite charge. (Note that electric charge is conserved in this process. See Section 37–5.)

The Sun radiates energy at a rate of about 4 x 10²⁶ W.

(a) At what rate is the Sun’s mass decreasing?

(b) How long does it take for the Sun to lose a mass equal to that of Earth?

(c) Estimate how long the Sun could last if it radiated constantly at this rate.

How much energy would be required to break a helium nucleus into its constituents, two protons and two neutrons? The rest masses of a proton (including an electron), a neutron, and neutral helium are, respectively, 1.00783 u, 1.00867 u, and 4.00260 u. (This energy difference is called the total binding energy of the ${}_2^4\text{He}$ nucleus.)

Two protons, each having a speed of 0.945c in the laboratory, are moving toward each other. Determine (a) the momentum of each proton in the laboratory, (b) the total momentum of the two protons in the laboratory, and (c) the momentum of one proton as seen by the other proton.

A pi meson of mass m_π decays at rest into a muon (mass m_μ) and a neutrino of negligible or zero mass. Show that the kinetic energy of the muon is K_μ = (m_π - m_μ)² c² / (2m_π).

A quasar emits familiar hydrogen lines whose wavelengths are 8.5% longer than what we measure in the laboratory.

(a) Using the Doppler formula for light, estimate the speed of this quasar.

(b) What result would you obtain if you used the “classical” Doppler shift discussed in Chapter 16?

A spaceship and its occupants have a total mass of 160,000 kg. The occupants would like to travel to a star that is 32 light-years away at a speed of 0.70c. To accelerate, the engine of the spaceship changes mass directly to energy.

(a) Estimate how much mass will be converted to energy to accelerate the spaceship to this speed.

(b) Assuming the acceleration is rapid, so the speed for the entire trip can be taken to be 0.70c, determine how long the trip will take according to the astronauts on board.

For a 1.0-kg mass, make a plot of the kinetic energy as a function of speed for speeds from 0 to 0.9c, using both the classical formula ( K = 1/2 mv²) and the correct relativistic formula ( K = ( γ -1)mc²).

Using Example 36–2 as a guide, show that for objects that move slowly in comparison to c, the length contraction formula is roughly ℓ ≈ ℓ₀ (1 - 1/2 v²/c²) . Use this approximation to find the “length shortening” ∆ℓ = ℓ₀ - ℓ of the train in Example 36–6 if the train travels at 100 km/h (rather than 0.92c).

Astronomers measure the distance to a particular star to be 6.0 light-years (1ly = distance light travels in 1 year). A spaceship travels from Earth to the vicinity of this star at steady speed, arriving in 3.25 years as measured by clocks on the spaceship. (a) How long does the trip take as measured by clocks in Earth’s reference frame? (b) What distance does the spaceship travel as measured in its own reference frame?

What magnetic field B is needed to keep 998-GeV protons revolving in a circle of radius 1.0km? Use the relativistic mass. The proton’s “rest mass” is 0.938 GeV/c². ( 1 GeV = 10⁹ eV.) [Hint: In relativity, mᵣₑₗ v²/r = qvB is still valid in a magnetic field, where mᵣₑₗ = γm.]