A sharp image is located 373 mm behind a 235-mm-focal-length converging lens. Find the object distance by calculation.

A 105-mm-focal-length lens is used to focus an image on the sensor of a camera. The maximum distance allowed between the lens and the sensor plane is 132 mm.

(a) How far in front of the sensor should the lens (assumed thin) be positioned if the object to be photographed is 10.0 m away? (b) 3.0 m away? (c) 1.0 m away?

(d) What is the closest object this lens could photograph sharply?

It is desired to magnify reading material by a factor of 3.0 x when a book is placed 9.0 cm behind a lens.

(a) Draw a ray diagram and describe the type of image this would be.

(b) What type of lens is needed?

(c) What is the power of the lens in diopters?

An object is located 1.35 m from an 8.0-D lens. By how much does the image move if the object is moved (a) 0.90 m closer to the lens, and (b) 0.90 m farther from the lens?

(II) In a film projector, the film acts as the object whose image is projected on a screen (Fig. 33–46). If a 105-mm-focal-length lens is to project an image on a screen 22.5 m away, how far from the lens should the film be? If the film is 24 mm wide, how wide will the picture be on the screen?

(III) A bright object is placed on one side of a converging lens of focal length f, and a white screen for viewing the image is on the opposite side. The distance d_T = d_i + d_o between the object and the screen is kept fixed, but the lens can be moved. Determine a formula for the distance between the two lens positions in part (a), and the ratio of the image sizes.

Two 28.0-cm-focal-length converging lenses are placed 16.5 cm apart. An object is placed 35.0 cm in front of one lens.

(a) Where will the final image formed by the second lens be located?

(b) What is the total magnification?

A diverging lens with ƒ = -36.5 cm is placed 14.0 cm behind a converging lens with ƒ = 20.0cm. Where will an object at infinity be focused?

(II) A diverging lens is placed next to a converging lens of focal length ƒ_C , as in Fig. 33–14. If ƒ_T represents the focal length of the combination, show that the focal length of the diverging lens, ƒ_D , is given by

1/ƒ_D = (1/ƒ_T) - (1/ƒ_C)

An object is placed 96.0 cm from a glass lens (n = 1.52) with one concave surface of radius 22.0 cm and one convex surface of radius 18.5 cm.

(a) Where is the final image?

(b) What is the magnification?

"(II) Two plane mirrors meet at a 135° angle, Fig. 32–47. If light rays strike one mirror at 32° as shown, at what angle θ do they leave the second mirror?

<IMAGE>"

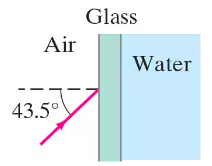
(II) An aquarium filled with water has flat glass sides whose index of refraction is 1.51. A beam of light from outside the aquarium strikes the glass at a 43.5° angle to the perpendicular (Fig. 32–52). What is the angle of this light ray when it enters (a) the glass, and then (b) the water? (c) What would be the refracted angle if the ray entered the water directly?

(II) (a) What is the minimum index of refraction for a glass or plastic prism to be used in binoculars (Fig. 32–34) so that total internal reflection occurs at 45°? (b) Will binoculars work if their prisms (assume n = 1.58) are immersed in water? (c) What minimum n is needed if the prisms are immersed in water?

A series of polarizers are each rotated 10° from the previous polarizer. Unpolarized light is incident on this series of polarizers. How many polarizers does the light have to go through before it is 1/6 of its original intensity?

(II) A planoconvex lens (Fig. 33–2a) has one flat surface and the other has R = 15.3 cm. This lens is used to view a red and yellow object which is 62.0 cm away from the lens. The index of refraction of the glass is 1.5106 for red light and 1.5226 for yellow light. What are the locations of the red and yellow images formed by the lens?

Figure 33–49 is a photograph of an eyeball with the image of a boy in a doorway. (a) Is the eye here acting as a lens or as a mirror? (b) Is the eye being viewed right side up or is the camera taking this photo upside down? (c) Explain, based on all possible images made by a convex mirror or lens.

<IMAGE>

As early morning passed toward midday, and the sunlight got more intense, a photographer noted that, if she kept her shutter speed constant, she had to change the f-number from f/5.6 to f/16. By what factor had the sunlight intensity increased during that time?

A physicist lost in the mountains tries to make a telescope using the lenses from his reading glasses. They have powers of +2.0 D and +4.5 D, respectively.

(a) What maximum magnification telescope is possible?

(b) Which lens should be used as the eyepiece?

A 50-year-old man uses +2.5 D lenses to read a newspaper 25 cm away. Ten years later, he must hold the paper 32 cm away to see clearly with the same lenses. What power lenses does he need now in order to hold the paper 25 cm away? (Distances are measured from the lens.)

An astronomical telescope, Fig. 33–36, produces an inverted image. One way to make a telescope that produces an upright image is to insert a third lens between the objective and the eyepiece, Fig. 33–39b. To have the same magnification, the non-inverting telescope will be longer. Suppose lenses of focal length 150 cm, 1.5 cm, and 10 cm are available. Where should these three lenses be placed to make a non-inverting telescope with magnification 100x?

The focal length f of a converging lens can be found by placing an object of known size at various locations in front of the lens and measuring the resulting real-image distances dᵢ and their associated magnifications m (minus sign indicates that image is inverted). The data taken in such an experiment are given here:

(a) Show algebraically that a graph of m vs. dᵢ should produce a straight line. What are the theoretically expected values for the slope and the y-intercept of this line? [Hint: dₒ is not constant.] (b) Using the data above, graph m vs. dᵢ and show that a straight line does indeed result. Use the slope of this line to determine the focal length of the lens. Does the y-intercept of your plot have the expected value?