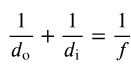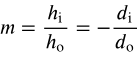Suppose that you want to take a photograph of yourself as you look at your image in a mirror 2.4 m away. For what distance should the camera lens be focused?

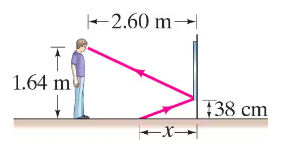
A person whose eyes are 1.64 m above the floor stands 2.60 m in front of a vertical plane mirror whose bottom edge is 38 cm above the floor, Fig. 32–48. What is the horizontal distance x, from the base of the wall supporting the mirror to the nearest point on the floor that can be seen reflected in the mirror?

Suppose you are 96 cm from a plane mirror. What area of the mirror is used to reflect the rays entering one eye from a point on the tip of your nose if your pupil diameter is 4.5 mm?

The lateral magnification of a convex mirror is +0.75 for objects 3.2 m from the mirror. What is the focal length of this mirror?

You look at yourself in a shiny 8.4-cm-diameter Christmas tree ball. If your face is 25.0 cm away from the ball’s front surface, where is your image? Is it real or virtual? Is it upright or inverted?

A dentist wants a small mirror that, when 2.00 cm from a tooth, will produce a 3.0 x upright image. What kind of mirror must be used and what must its radius of curvature be?

An object 4.0 mm high is placed 18 cm from a convex mirror of radius of curvature 18 cm. Show by ray tracing that the image is virtual, and estimate the image distance.

An object 4.0 mm high is placed 18 cm from a convex mirror of radius of curvature 18 cm. Show that the (negative) image distance can be computed from Eq. 32–2 using a focal length of -9.0 cm.

An object 4.0 mm high is placed 18 cm from a convex mirror of radius of curvature 18 cm. Compute the image size, using Eq. 32–3.

(II) Show, using a ray diagram, that the lateral magnification m of a convex mirror is m = -dᵢ/dₒ , just as for a concave mirror. [Hint: Consider a ray from the top of the object that reflects at the center of the mirror.]

In Example 32–4, show that if the object is moved 10.0 cm farther from the concave mirror, the object’s image size will equal the object’s actual size. Stated as a multiple of the focal length, what is the object distance for this “actual-sized image” situation?

Let the focal length of a convex mirror be written as ƒ = ―|ƒ|. Show that the lateral magnification m of an object a distance dₒ from this mirror is given by m = |ƒ| / (dₒ +|ƒ| ). Based on this relation, explain why your nose looks bigger than the rest of your face when looking into a convex mirror.

When walking toward a concave mirror you notice that your image flips at a distance of 0.80 m from the mirror. What is the radius of curvature of the mirror? [Hint: Carefully examine Section 32–4.]

A shaving or makeup mirror is designed to magnify your face by a factor of 1.8 (when compared to a flat mirror) when your face is placed 20.0 cm in front of it.

(a) What type of mirror is it?

(b) Describe the type of image that it makes of your face.

(c) Calculate the required radius of curvature for the mirror.

An object is placed a distance r in front of a wall, where r exactly equals the radius of curvature of a certain concave mirror. At what distance from the wall should this mirror be placed so that a real image of the object is formed on the wall? What is the lateral magnification of the image?

A flashlight beam strikes the surface of a pane of glass (n = 1.56) at a 69° angle to the normal. What is the angle of refraction?

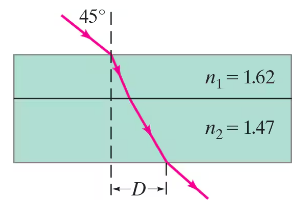
A light beam strikes a 2.5-cm-thick piece of plastic with a refractive index of 1.62 at a 45° angle. The plastic is on top of a 3.8-cm-thick piece of glass for which n = 1.47. What is the distance D in Fig. 32–51?

(II) In searching the bottom of a pool at night, a watchman shines a narrow beam of light from his flashlight, 1.3 m above the water level, onto the surface of the water at a point 2.8 m from his foot at the edge of the pool (Fig. 32–53). Where does the spot of light hit the bottom of the pool which is 2.1 m deep? Measure from the bottom of the wall beneath his foot.

<IMAGE>

(III) A light ray is incident on a flat piece of glass with index of refraction n as in Fig. 32–24. Show that if the incident angle θ is small, the emerging ray is displaced a distance d = tθ(n - 1)/n , where t is the thickness of the glass, θ is in radians, and d is the perpendicular distance between the incident ray and the (dashed) line of the emerging ray (Fig. 32–24).

A light beam strikes a piece of glass at a 55.00° incident angle. The beam contains two wavelengths, 450.0 nm and 700.0 nm, for which the index of refraction of the glass is 1.4831 and 1.4754, respectively. What is the angle between the two refracted beams?

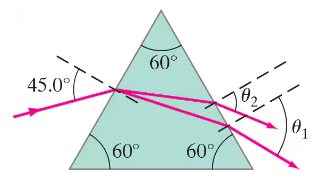
A parallel beam of light containing two wavelengths, λ₁ = 461 nm and λ₂ = 656 nm, enters the silicate flint glass of an equilateral prism as shown in Fig. 32–56. At what angle does each beam leave the prism (give angle with normal to the face)? See Fig. 32–28.

The critical angle for a certain liquid–air surface is 52.6°. What is the index of refraction of the liquid?

(II) A ray of light, after entering a light fiber, reflects at an angle of 14.5° with the long axis of the fiber, as in Fig. 32–57. Calculate the distance along the axis of the fiber that the light ray travels between successive reflections off the sides of the fiber. Assume that the fiber has an index of refraction of 1.55 and is 1.60 x 10^-4 m in diameter.

A beam of light is emitted 7.7 cm beneath the surface of a liquid and strikes the surface 7.2 cm from the point directly above the source. If total internal reflection occurs, what can you say about the index of refraction of the liquid?

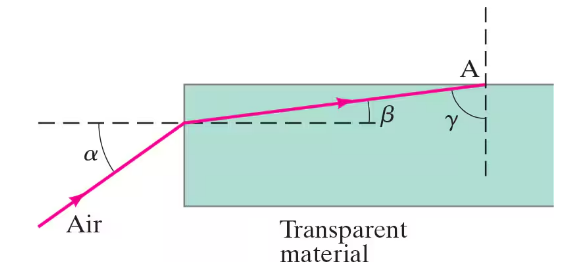
(III) A beam of light enters the end of an optic fiber as shown in Fig. 32–59. (a) Show that we can guarantee total internal reflection at the side surface of the material (at point A), if the index of refraction is greater than about 1.42. In other words, regardless of the angle α , the light beam reflects back into the material at point A, assuming air outside. (b) What if the fiber is immersed in water?

A fish is swimming in water inside a thin spherical glass bowl of uniform thickness. Assuming the radius of curvature of the bowl is 32.0 cm, locate the image of the fish if the fish is located: (a) at the center of the bowl; (b) 20.0 cm from the side of the bowl between the observer and the center of the bowl. Assume the fish is small.

Two identical concave mirrors are set facing each other 1.0 m apart. A small lightbulb is placed halfway between the mirrors. A small piece of paper placed just to the left of the bulb prevents light from the bulb from directly shining on the left mirror, but light reflected from the right mirror still reaches the left mirror. A good image of the bulb appears on the left side of the piece of paper. What is the focal length of the mirrors?

(c) Determine the magnification of a plane mirror in this same limit.

(d) Are your results in parts (b) and (c) consistent with the discussion of Section 32–2 on plane mirrors?

The critical angle of a certain piece of plastic in air is θ_C = 35.8°. What is the critical angle of the same plastic if it is immersed in water?

Two plane mirrors are facing each other 2.2 m apart as in Fig. 32–60. You stand 1.5 m away from one of these mirrors and look into it. You will see multiple images of yourself. (a) How far away from you are the first three images of yourself in the mirror in front of you? (b) Are these first three images facing toward you or away from you?

<IMAGE>