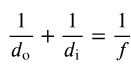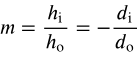Suppose that you want to take a photograph of yourself as you look at your image in a mirror 2.4 m away. For what distance should the camera lens be focused?

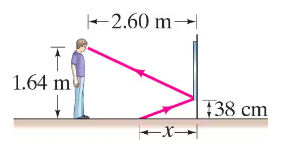
A person whose eyes are 1.64 m above the floor stands 2.60 m in front of a vertical plane mirror whose bottom edge is 38 cm above the floor, Fig. 32–48. What is the horizontal distance x, from the base of the wall supporting the mirror to the nearest point on the floor that can be seen reflected in the mirror?

Suppose you are 96 cm from a plane mirror. What area of the mirror is used to reflect the rays entering one eye from a point on the tip of your nose if your pupil diameter is 4.5 mm?

The lateral magnification of a convex mirror is +0.75 for objects 3.2 m from the mirror. What is the focal length of this mirror?

You look at yourself in a shiny 8.4-cm-diameter Christmas tree ball. If your face is 25.0 cm away from the ball’s front surface, where is your image? Is it real or virtual? Is it upright or inverted?

A dentist wants a small mirror that, when 2.00 cm from a tooth, will produce a 3.0 x upright image. What kind of mirror must be used and what must its radius of curvature be?

An object 4.0 mm high is placed 18 cm from a convex mirror of radius of curvature 18 cm. Show by ray tracing that the image is virtual, and estimate the image distance.

An object 4.0 mm high is placed 18 cm from a convex mirror of radius of curvature 18 cm. Show that the (negative) image distance can be computed from Eq. 32–2 using a focal length of -9.0 cm.

An object 4.0 mm high is placed 18 cm from a convex mirror of radius of curvature 18 cm. Compute the image size, using Eq. 32–3.

(II) Show, using a ray diagram, that the lateral magnification m of a convex mirror is m = -dᵢ/dₒ , just as for a concave mirror. [Hint: Consider a ray from the top of the object that reflects at the center of the mirror.]

In Example 32–4, show that if the object is moved 10.0 cm farther from the concave mirror, the object’s image size will equal the object’s actual size. Stated as a multiple of the focal length, what is the object distance for this “actual-sized image” situation?

Let the focal length of a convex mirror be written as ƒ = ―|ƒ|. Show that the lateral magnification m of an object a distance dₒ from this mirror is given by m = |ƒ| / (dₒ +|ƒ| ). Based on this relation, explain why your nose looks bigger than the rest of your face when looking into a convex mirror.

When walking toward a concave mirror you notice that your image flips at a distance of 0.80 m from the mirror. What is the radius of curvature of the mirror? [Hint: Carefully examine Section 32–4.]