Back
BackProblem 5
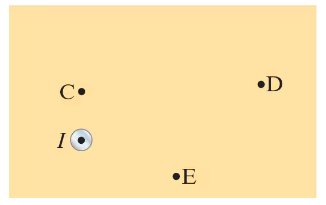
(II) In Fig. 28–36, a long straight wire carries current I out of the page toward you. Indicate, with appropriate arrows, the direction and (relative) magnitude of at each of the points C, D, and E in the plane of the page.
Problem 7
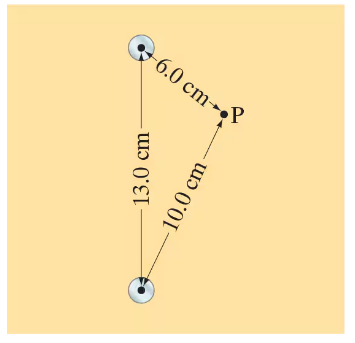
(II) Two long thin parallel wires 13.0 cm apart carry 25-A currents in the same direction. Determine the magnetic field vector at a point 10.0 cm from one wire and 6.0 cm from the other (Fig. 28–37). [Hint: You could try using the law of cosines, Appendix A.]
Problem 13
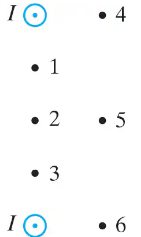
(II) Two long straight wires each carry a dc current I out of the page toward the viewer, Fig. 28–38. Indicate, with appropriate arrows, the direction of at each of the points 1 to 6 in the plane of the page. State if the field is zero at any of the points.
Problem 18
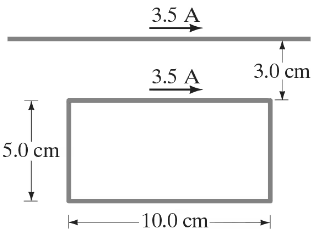
"(II) A rectangular loop of wire is placed next to a straight wire, as shown in Fig. 28–40. There is a dc current of 3.5 A in both wires. Determine the magnitude and direction of the net force on the loop.
Problem 19
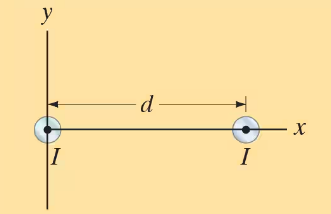
(II) Let two long parallel wires, a distance d apart, carry equal dc currents I in the same direction. One wire is at 𝓍 = 0, the other at 𝓍 = d, Fig. 28–41. Determine along the 𝓍 axis between the wires as a function of 𝓍.
Problem 21
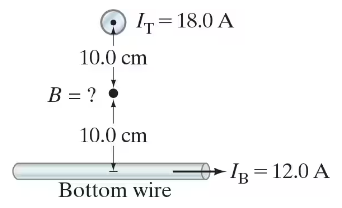
(II) Two long wires are oriented so that they are perpendicular to each other. At their closest, they are 20.0 cm apart (Fig. 28–42). What is the magnitude of the magnetic field at a point midway between them if the top one carries a current of 18.0 A and the bottom one carries 12.0 A?
Problem 23
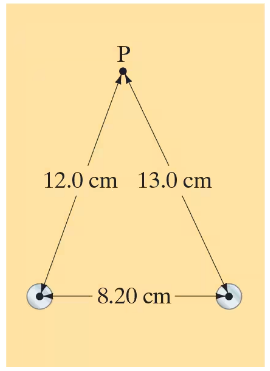
(II) Two long parallel wires 8.20 cm apart carry 19.5-A dc currents in the same direction. Determine the magnetic field vector at a point P, 12.0 cm from one wire and 13.0 cm from the other. See Fig. 28–43. [Hint: Use the law of cosines. See Appendix A or inside rear cover.]
Problem 33
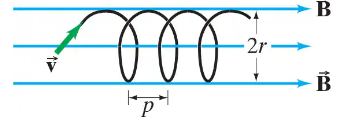
(II) An electron enters a uniform magnetic field B = 0.28 T at a 45° angle to . Determine the radius r and pitch p (distance between loops) of the electron’s helical path assuming its speed is 2.2 x 106 m/s. See Fig. 27–48.
Problem 34
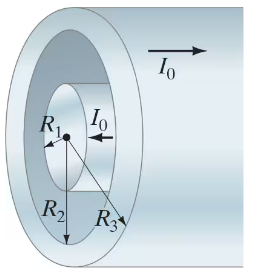
(III) A coaxial cable consists of a solid inner conductor of radius R1, surrounded by a concentric cylindrical tube of inner radius R2 and outer radius R3 (Fig. 28–45). The conductors carry equal and opposite currents I₀ distributed uniformly across their cross sections. Determine the magnetic field at a distance R from the axis for: (a) R < R1; (b) R1 < R < R2; (c) R2 < R < R3; (d) R > R3. (e) Let I₀ = 1.50 A, R1 = 1.00 cm , R2 = 2.00 cm , and R3 = 2.50 cm Graph B from R = 0 to R = 3.00 cm.
Problem 38
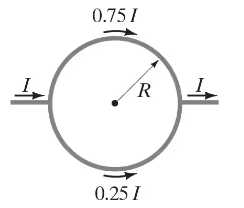
(II) A circular conducting ring of radius 𝑅 is connected to two exterior straight wires at two ends of a diameter (Fig. 28–47). The current I splits into unequal portions as shown (unequal resistance) while passing through the ring. What is at the center of the ring?
Problem 40
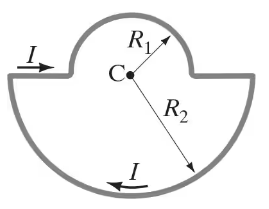
(II) A wire is formed into the shape of two half circles connected by equal-length straight sections as shown in Fig. 28–48. A current I flows in the circuit clockwise as shown. Determine (a) the magnitude and direction of the magnetic field at the center, C, and (b) the magnetic dipole moment of the circuit.
Problem 43
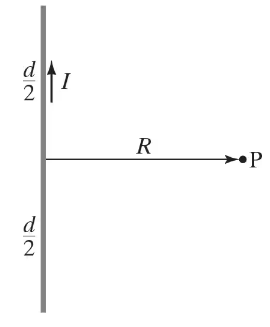
(II) Consider a straight section of wire of length d, as in Fig. 28–51, which carries a current I. (a) Show that the magnetic field at a point P a distance 𝑅 from the wire along its perpendicular bisector is
(b) Show that this is consistent with Example 28–10 for an infinite wire.
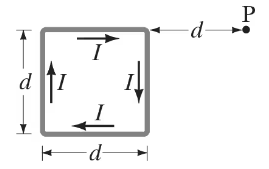
Problem 45
(III) Use the result of Problem 44 to find the magnetic field at point P in Fig. 28–53 due to the current in the square loop.
Problem 49
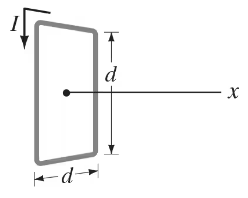
(III) A square loop of wire, of side d, carries a current I. (a) Determine the magnetic field B at points on a line (call it the 𝓍 axis) perpendicular to the plane of the square which passes through the center of the square (Fig. 28–56). Express B as a function of 𝓍, the distance from the center of the square. (b) For 𝓍 ≫ d, does the square appear to be a magnetic dipole? If so, what is its dipole moment?
Problem 55
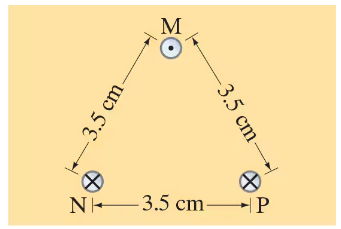
Three long parallel wires are 3.5 cm from one another. (Looking along them, they are at three corners of an equilateral triangle.) The current in each wire is 9.50 A, but its direction in wire M is opposite to that in wires N and P (Fig. 28–57). Determine the magnetic force per unit length on each wire due to the other two.
Problem 57
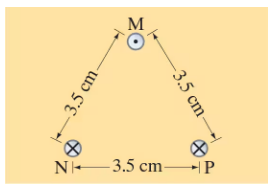
In Fig. 28–57 the top wire is 1.00-mm-diameter copper wire and is suspended in air due to the two magnetic forces from the bottom two wires. The current is 35.0 A in each of the two bottom wires. Calculate the required current in the suspended wire (M).
Problem 61
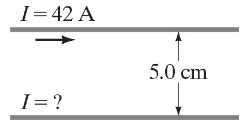
A long horizontal wire carries a current of 42 A. A second wire, made of 1.00-mm-diameter copper wire and parallel to the first, is kept in suspension magnetically 5.0 cm below (Fig. 28–60). (a) Determine the magnitude and direction of the current in the lower wire. (b) Is the lower wire in stable equilibrium? (c) Repeat parts (a) and (b) if the second wire is suspended 5.0 cm above the first due to the first’s magnetic field.
Problem 62
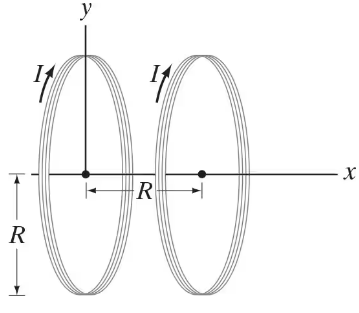
Helmholtz coils are two identical circular coils having the same radius 𝑅 and the same number of turns N, separated by a distance equal to the radius 𝑅 and carrying the same dc current I in the same direction. (See Fig. 28–61.) They are used in scientific instruments to generate nearly uniform magnetic fields. (They can be seen in the photo, Fig. 27–19.) (a) Determine the magnetic field B at points 𝓍 along the line joining their centers. Let 𝓍 = 0 at the center of one coil, and 𝓍 = 𝑅 at the center of the other. (b) Show that the field midway between the coils is particularly uniform by showing that dB/d𝓍 = 0 and d²B/d𝓍² = 0 at the midpoint between the coils. (c) If 𝑅 = 10.0 cm, N = 85 turns and I = 3.0 A, what is the field at the midpoint between the coils, 𝓍 = 𝑅/2?
Problem 63b
A set of Helmholtz coils (see Problem 62, Fig. 28–61) have a radius 𝑅 = 10.0 cm and are separated by a distance 𝑅 = 10.0 cm . Each coil has 85 loops carrying a current I = 2.0 A. Graph B as a function of 𝓍.
Problem 74
You want to get an idea of the magnitude of magnetic fields produced by overhead power lines. You estimate that a transmission wire is about 12 m above the ground. The local power company tells you that the lines operate at 145 kV and provide a maximum of 45 MW to the local area. Estimate the maximum magnetic field you might experience walking under one such power line, and compare to the Earth’s field. [For an ac current, values are rms, and the magnetic field will be changing.]
Problem 77
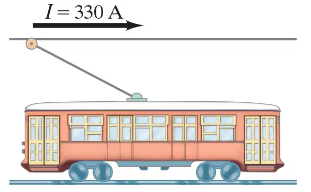
The power cable for an electric trolley (Fig. 27–60) carries a horizontal current of 330 A toward the east. The Earth’s magnetic field has a strength 5.0 x 10-5 T and makes an angle of dip of 22° at this location. Calculate the magnitude and direction of the magnetic force on a 15-m length of this cable.
Problem 77a
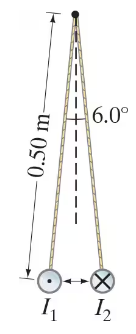
Two long straight aluminum wires, each of diameter 0.42 mm, carry the same current but in opposite directions. They are suspended by 0.50-m-long strings as shown in Fig. 28–66. If the suspension strings make an angle of 3.0° with the vertical and are hanging freely, what is the current in the wires?
Problem 79
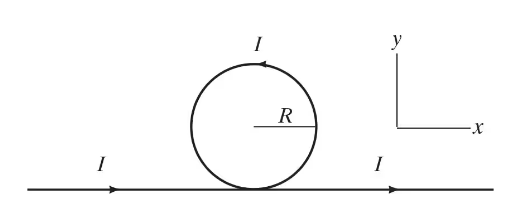
Part of a long, thin insulated straight wire is formed into a single circular loop of radius 𝑅 (Fig. 28–68) and carries a current I. (a) What is the magnitude and direction of the magnetic field at the center of the loop? (b) If the plane of the loop is twisted 90 degrees so that the plane is perpendicular to the straight part of the wire (i.e., in the yz plane) what is the magnitude and direction of the field now at the center of the loop?
Problem 80
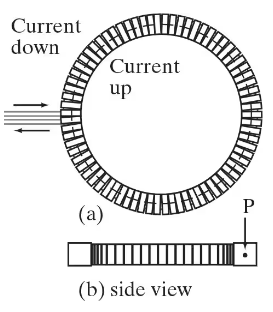
A toroid is fabricated with a circular shape and loops with a square cross section as shown in Fig. 28–69. The cross-section of a loop is a square of side 6.0 cm. The inner radius of the whole circular toroid is 3.0 m. There are 320 loops of wire which carry a 45-A dc current using a nearby power supply at 20.0 V. The arrows show the current flow in and out of the toroid. The current flows up at the inner diameter and down at the outer diameter. (a) Calculate the strength of the magnetic field at the center of the square’s cross section at point P. (b) Is the magnetic field pointing clockwise or counterclockwise? (c) The square cross-sectional area of the wire is uniformly 0.10 cm2. What is the resistivity of the wire?