Back
BackProblem ]11
A stiff wire 50.0 cm long is bent at a right angle in the middle. One section lies along the z axis and the other is along the line y = 2x in the xy plane. A current of 20.0 A flows in the wire—down the z axis and out the wire in the xy plane. The wire passes through a uniform magnetic field given by = (0.285î ) T. Determine the magnitude and direction of the total force on the wire.
Problem 3
(a) What is the force per meter of length on a straight wire carrying a 7.40-A current when perpendicular to a 0.90-T uniform magnetic field?
(b) What if the angle between the wire and field is 35.0°?
Problem 7
The magnetic force per meter on a wire is measured to be only 55% of its maximum possible value. What is the angle between the wire and the magnetic field?
Problem 14
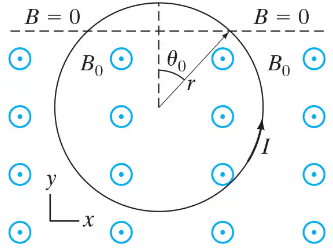
(II) A current-carrying circular loop of wire (radius r, current I) is partially immersed in a magnetic field of constant magnitude B₀ directed out of the page as shown in Fig. 27–43. Determine the net force on the loop due to the field in terms of θ₀. (Note that θ₀ points to the dashed line, above which B = 0.)
Problem 15
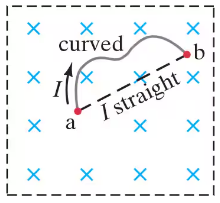
(III) A curved wire, connecting two points a and b, lies in a plane perpendicular to a uniform magnetic field and carries a current I. Show that the resultant magnetic force on the wire, no matter what its shape, is the same as that on a straight wire connecting the two points carrying the same current I. See Fig. 27–44.
Problem 23
A 720-KeV (kinetic energy) proton enters a 0.20-T field, in a plane perpendicular to the field. What is the radius of its path? See Section 23–8.
Problem 27
A particle of charge q moves in a circular path of radius r in a uniform magnetic field . If the magnitude of the magnetic field is doubled, and the kinetic energy of the particle remains constant, what happens to the angular momentum of the particle?
Problem 30
For a particle of mass m and charge q moving in a circular path in a magnetic field B, (a) show that its kinetic energy is proportional to r², the square of the radius of curvature of its path. Show that its angular momentum is L=qBr² , around the center of the circle.
Problem 40
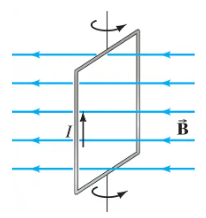
How much work is required to rotate the current loop (Fig. 27–23) in a uniform magnetic field from (a) θ = 0° ( ∣∣ ) to θ = 180°, (b) θ = 90° to θ = -90°.
Problem 41
A circular coil 18.0 cm in diameter and containing twelve loops lies flat on the ground. The Earth’s magnetic field at this location has magnitude 5.50 x 10⁻⁵ T and points into the Earth at an angle of 54.0° below a line pointing due north. If a 7.10-A clockwise current passes through the coil, (a) determine the torque on the coil; (b) which edge of the coil rises up : north, east, south, or west?
Problem 48
\What is the value of q/m for a particle that moves in a circle of radius 8.0 mm in a 0.46-T magnetic field if a crossed 320-V/m electric field will make the path straight?
Problem 53
A long copper strip is 3.0 cm wide and thick. When it carries a steady 42-A current in a 0.80-T magnetic field it produces a 6.5-μV Hall emf. Determine:
(a) the Hall field in the conductor;
(b) the drift speed of the conduction electrons;
(c) the density of free electrons in the metal.
Problem 56
In a mass spectrometer, germanium atoms have radii of curvature equal to 21.0, 21.6, 21.9, 22.2, and 22.8 cm. The largest radius corresponds to an atomic mass of 76 u. What are the atomic masses of the other isotopes?
Problem 57
One form of mass spectrometer accelerates ions by a voltage V before they enter a magnetic field B. The ions are assumed to start from rest. Show that the mass of an ion is m = qB²R²/2V, where R is the radius of the ions’ path in the magnetic field and q is their charge.
Problem 58b
Suppose the electric field between the electric plates in the mass spectrometer of Fig. 27–34 is 2.84 x 10⁴ V/m and the magnetic fields are B = B'= 0.58 T. The source contains carbon isotopes of mass numbers 12, 13, and 14 from a long-dead piece of a tree. (To estimate atomic masses, multiply by 1.67 x 10⁻²⁷ kg .) How far apart are the marks formed by the singly charged ions of each type on a detector or photographic film? What if the ions were doubly charged?
Problem 58c
Suppose the electric field between the electric plates in the mass spectrometer of Fig. 27–34 is 2.84 x 10⁴ V/m and the magnetic fields are B = B'= 0.58 T. The source contains carbon isotopes of mass numbers 12, 13, and 14 from a long-dead piece of a tree. (To estimate atomic masses, multiply by 1.67 x 10⁻²⁷ kg.) Does it matter if the ion charge is positive (lost electrons) or negative (gained electrons)? Explain.
Problem 61
A mass spectrometer is monitoring air pollutants. It is difficult, however, to separate molecules of nearly equal mass such as CO (28.0106 u) and N₂ (28.0134 u). How large a radius of curvature must a spectrometer have (Fig. 27–34) if these two molecules are to be separated on the detector by 0.50 mm?
Problem 66
Near the equator, the Earth’s magnetic field points almost horizontally to the north and has magnitude B = 0.50 x 10⁻⁴ T. What should be the magnitude and direction for the velocity of an electron if its weight is to be exactly balanced by the magnetic force?
Problem 67
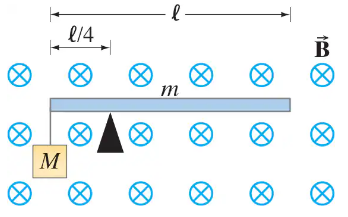
A uniform conducting rod of length ℓ and mass m sits atop a fulcrum, which is placed a distance ℓ/4 from the rod’s left-hand end and is immersed in a uniform magnetic field of magnitude B directed into the page (Fig. 27–54). An object whose mass M is 7.0 times greater than the rod’s mass is hung from the rod’s left-hand end. What current (direction and magnitude) should flow through the rod in order for it to be “balanced” (i.e., be at rest horizontally) on the fulcrum? (Flexible connecting wires which exert negligible force on the rod are not shown.)
Problem 71
The magnetic field B at the center of a circular coil of wire carrying a current I (as in Fig. 27–9) is B = (μ₀NI) / 2r where N is the number of loops in the coil and r is its radius. Imagine a simple model in which the Earth’s magnetic field of about 1 G ( = 1 x 10⁻⁴ T) near the poles is produced by a single current loop around the equator. Roughly estimate the current this loop would carry.
Problem 76
Suppose the Earth’s magnetic field at the equator has magnitude 0.50 x 10⁻⁴ T and a northerly direction at all points. Estimate the speed a singly ionized uranium ion ( m = 238 u, q = e) would need to circle the Earth 5.0 km above the equator. Can you ignore gravity? [Ignore relativity.]