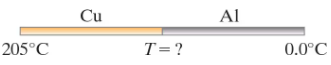Back
BackProblem 3
An average active person consumes about 2500 Cal a day.
(a) What is this in joules?
(b) What is this in kilowatt-hours?
(c) If your power company charges about per kilowatt-hour, how much would your energy cost per day if you bought it from the power company? Could you feed yourself on this much money per day?
Problem 9
What is the specific heat of a metal substance if 165 kJ of heat is needed to raise 4.1 kg of the metal from 18.0°C to 37.2°C?
Problem 11
(a) How long does it take a 750-W coffeepot to bring to a boil 0.75 L of water at sea level initially at 11°C? Assume that the part of the pot which is heated with the water is made of 250 g of aluminum, and that no water boils away.
(b) For how long could this amount of energy run a 60-W lightbulb?
Problem 16c
The heat capacity, C, of an object is defined as the amount of heat needed to raise its temperature by 1 °C. Thus, to raise the temperature by ∆T requires heat Q given by Q = C∆T. What is the heat capacity of 38 kg of water?
Problem 18
A 215-g sample of a substance is heated to 330°C and then plunged into a 105-g aluminum calorimeter cup containing 185 g of water and a 17-g glass thermometer at 10.5°C. The final temperature is 35.0°C. What is the specific heat of the substance? (Assume no water boils away.)
Problem 19
A 0.095-kg aluminum sphere is dropped from the roof of a 55-m-high building. If 65% of the thermal energy produced when it hits the ground is absorbed by the sphere, what is its temperature increase?
Problem 19.14
(II) A 0.40-kg iron horseshoe just forged and very hot (Fig. 19–31), is dropped into 1.35 L of water in a 0.30-kg iron pot initially at 20.0°C. If the final equilibrium temperature is 25.0°C, estimate the initial temperature of the hot horseshoe..
<IMAGE>
Problem 19.31
(II) A cube of ice is taken from the freezer at -8.5°C and placed in an 85-g aluminum calorimeter filled with 310 g of water at room temperature of 20.0°C. The final situation is all water at 17.0°C. What was the mass of the ice cube?
Problem 20
If 3.40 x 10⁵ J of energy is supplied to a container of liquid oxygen at -183° C , how much oxygen can evaporate?
Problem 21
How much heat is needed to melt 26.50 kg of silver that is initially at 25°C?
Problem 22
What mass of steam at 100°C must be added to 1.00 kg of ice at 0°C to yield liquid water at 30°C?
Problem 25b
High-altitude mountain climbers do not eat snow, but always melt it first with a stove. To see why, calculate the energy absorbed from your body if you melt 1.0 kg of -15°C snow using a stove and drink the resulting 1.0 kg of water at 2°C, which your body has to warm to 37°C.
Problem 26b
An iron boiler of mass 180 kg contains 710 kg of water at 18°C. A heater supplies energy at the rate of 58,000 kJ/h. How long does it take for the water to all have changed to steam?
Problem 28
Determine the latent heat of fusion of mercury using the following calorimeter data: 1.00 kg of solid Hg at its melting point of −39.0°C is placed in a 0.620-kg aluminum calorimeter with 0.400 kg of water at 12.80°C; the resulting equilibrium temperature is 5.06°C.
Problem 29
At a crime scene, the forensic investigator notes that the 6.2-g lead bullet that was stopped in a doorframe apparently melted completely on impact. Assuming the bullet was shot at room temperature (20°C), what does the investigator calculate as the minimum muzzle velocity of the gun?
Problem 30
A 55-g bullet traveling at 250 m/s penetrates a block of ice at 0°C and comes to rest within the ice. Assuming that the temperature of the bullet doesn’t change appreciably, how much ice is melted as a result of the collision?
Problem 38b
A 1.0-L volume of air initially at 3.5 atm of (gauge)pressure is allowed to expand isothermally until the (gauge) pressure is 1.0 atm. It is then compressed at constant pressure to its initial volume, and lastly is brought back to its original pressure by heating at constant volume. How much work does the 1.0 L of air do in this process?
Problem 50
If a heater supplies 1.8 x 10⁶ J/h to a room 3.5 m x 4.6 m x 3.0 m containing air at 20°C and 1.0 atm, by how much will the temperature rise in one hour, assuming no losses of heat or air mass to the outside? Assume air is an ideal diatomic gas with molecular mass 29.
Problem 59
Show, using Eqs. 19–7 and 19–16, that the work done by a gas that slowly expands adiabatically from pressure P₁ and volume V₁ , to P₂ and V₂, is given by W = (P₁V₁ - P₂V₂) / (γ - 1).
Problem 70
A ceramic teapot (e = 0.70) and a shiny metal one (e = 0.10) each hold 0.55 L of tea at 85°C. (a) Estimate the rate of heat loss from each, and (b) estimate the temperature drop after 30 min for each. Consider only radiation, and assume the surroundings are at 20°C.
Problem 71
A copper rod and an aluminum rod of the same length and cross-sectional area are attached end to end (Fig. 19–35). The copper end is placed in a furnace maintained at a constant temperature of 205°C. The aluminum end is placed in an ice bath held at a constant temperature of 0.0°C. Calculate the temperature at the point where the two rods are joined.
Problem 75
(a) Estimate the total power radiated into space by the Sun, assuming it to be a perfect emitter at T = 5500 K. The Sun’s radius is 7.0 x 10⁸ m.
(b) From this, determine the power per unit area arriving at the Earth, 1.5 x 10¹¹ m away (Fig. 19–37).
Problem 77
What will be the final result when equal masses of ice at 0°C and steam at 100°C are mixed together?
Problem 85
A microwave oven is used to heat 250 g of water. On its maximum setting, the oven can raise the temperature of the liquid water from 20°C to 100°C in 1 min 45 s ( = 105 s).
(a) At what rate does the oven put energy into the liquid water?
(b) If the power input from the oven to the water remains constant, determine how many grams of water will boil away if the oven is operated for 2 min (rather than just 1 min 45 s).
Problem 86a
The temperature within the Earth’s crust increases about 1.0 C° for each 30 m of depth. The thermal conductivity of the crust is 0.80 J/s C°. Determine the heat transferred from the interior to the surface for the entire Earth in 1.0 h.
Problem 94
A diesel engine accomplishes ignition without a spark plug by an adiabatic compression of air to a temperature above the ignition temperature of the diesel fuel, which is injected into the cylinder at the peak of the compression. Suppose air is taken into the cylinder at 280 K and volume V₁ and is compressed adiabatically to 560° C ( ≈ 1000 °F) and volume V₂. Assuming that the air behaves as an ideal gas whose ratio of CP to CV is 1.4, calculate the compression ratio V₁/ V₂ of the engine.
Problem 99a
Calculate what will happen when 1000 J of heat is added to 100 grams of ice at -20°C.
Problem 99d
Calculate what will happen when 1000 J of heat is added to 100 grams of water at 100°C.
Problem 100b
A 12-g lead bullet traveling at 220 m/s passes through a thin wall and emerges at a speed of 160 m/s. If the bullet absorbs 50% of the heat generated, If the bullet’s initial temperature was 20°C, will any of the bullet melt, and if so, how much?
Problem 101a
A leaf of area 40cm² and mass 4.5 x 10⁻⁴ kg directly faces the Sun on a clear day. The leaf has an emissivity of 0.85 and a specific heat of 0.80 kcal/kgK. Estimate the energy absorbed per second by the leaf from the Sun.