Back
BackProblem 7a
A 1.0-mol sample of helium gas has a temperature of 18°C. What is the total kinetic energy of all the gas atoms in the sample?
Problem 19
Estimate how many air molecules rebound from a wall in a typical room per second, assuming an ideal gas of N molecules contained in a cubic room with sides of length ℓ at temperature T and pressure P.
(a) Show that the frequency f with which gas molecules strike a wall is ƒ = ( /2)(P/kT) ℓ² where is the average x component of the molecule’s velocity.
(b) Show that the equation can then be written as ƒ≈ Pℓ² / where m is the mass of a gas molecule.
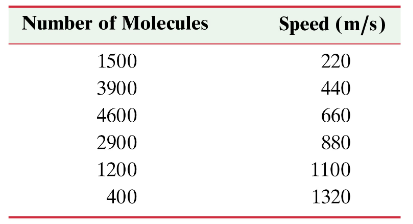
Problem 22a
A gas consisting of 14,500 molecules, each of mass 2.00 x 10⁻²⁶ kg, has the following distribution of speeds, which crudely mimics the Maxwell distribution. Determine vᵣₘₛ for this distribution of speeds.
Problem 25b
For what range of pressures and temperatures can CO₂ be a liquid? Refer to Fig. 18-6.
Problem 26a
Water is in which phase when the pressure is 0.01 atm and the temperature is 90°C?
Problem 45
Below a certain threshold pressure, the air molecules (0.3-nm diameter) within a research vacuum chamber are in the “collision-free regime,” meaning that a particular air molecule is as likely to cross the container and collide with the opposite wall as it is to collide with another air molecule. Estimate the threshold pressure for a vacuum chamber of side 1.0 m at 20°C.
Problem 46a
At about what pressure would the mean free path of air molecules be 0.30 m? Assume T = 20° C.
Problem 46b
At about what pressure would the mean free path of air molecules be equal to the diameter of air molecules, ≈ 3 x 10⁻¹⁰ m? Assume T = 20° C.
Problem 54
Estimate the time needed for a glycine molecule (see Table 18–3) to diffuse a distance of 25μm in water at 20°C if its concentration varies over that distance from 1.00 mol/m³ to 0.50 mol/m³. Compare this “speed” to its rms (thermal) speed. The molecular mass of glycine is about 75 u.
Problem 61c
The escape speed from the Earth is 1.12 x 10⁴ m/s (Section 8–7). So a gas molecule traveling away from Earth near the outer boundary of the Earth’s atmosphere would, at this speed, be able to escape from the Earth’s gravitational field and be lost to the atmosphere. Can you explain why our atmosphere contains oxygen but not helium?
Problem 63b
A scuba tank has a volume of 3100 cm³. For very deep dives, the tank is filled with 50% (by volume) pure oxygen and 50% pure helium. What is the ratio of the average kinetic energies of the two types of molecule?
Problem 64
A sauna has 7.8 m³ of air volume, and the temperature is 85°C. The air is perfectly dry. How much water (in kg) should be evaporated if we want to increase the relative humidity from 0% to 10%? (See Table 18–2.)
Problem 69
A space vehicle returning from the Moon enters the Earth’s atmosphere at a speed of about 42,000 km/h. Molecules (assume nitrogen) striking the nose of the vehicle with this speed correspond to what temperature? (Because of this high temperature, the nose of a space vehicle must be made of special materials; indeed, part of it does vaporize, and this is seen as a bright blaze upon reentry.)
Problem 70a
Calculate the total water vapor pressure in the air on the following day: a hot summer day, with the temperature 30°C and the relative humidity at 75%.
Problem 71
At room temperature, it takes approximately 2.45 x 10³ J to evaporate 1.00 g of water. Estimate the average speed of evaporating molecules. What multiple of vrms (at 20°C) for water molecules is this? (Assume Eq. 18–4 holds.)
Problem 73b
A sample of cesium vapor is in an oven at 400°C. The volume of the oven is 75 cm³, the vapor pressure of Cs at 400°C is 17 mm-Hg, and the diameter of cesium atoms in the vapor is 0.33 nm. Determine the number of collisions a single Cs atom undergoes with other cesium atoms per second.
Problem 74
Using the ideal gas law, find an expression for the mean free path ℓM that involves pressure and temperature instead of (N/V). Use this expression to find the mean free path for nitrogen molecules at a pressure of 7.5 atm and 300 K.
Problem 77a
From the van der Waals equation of state, show that the critical temperature and pressure are given by Tcr = 8a / 27bR , Pcr = a / 27b². [Hint: Use the fact that the P versus V curve has an inflection point at the critical point so that the first and second derivatives are zero.]