Refrigeration units can be rated in “tons.” A 1-ton air conditioning system can remove sufficient energy to freeze 1 ton (2000 pounds = 909 kg) of 0°C water into 0°C ice in one 24-h day. Assume the hot part of a day averages 35°C and the interior of a house is maintained at 22°C by the continuous operation of a 6-ton air conditioning system for 6 hours a day. How much does this cooling cost the homeowner per day, and per month?Assume the work done by the refrigeration unit is powered by electricity that costs $0.13 per kWh and that the unit’s coefficient of performance is only 18% of an ideal refrigerator. 1 kWh = 3.60 x 10⁶ J .

A four-cylinder gasoline engine has an efficiency of 0.22 and delivers 180 J of work per cycle per cylinder. If the engine runs at 25 cycles per second (1500 rpm), determine the total heat input per second from the gasoline.

Assume that a 65-kg hiker needs to eat 4.0 x 10³ kcal of energy to supply a day’s worth of metabolism ( = Q_H). Estimate the elevation change the person can climb in one day, using only this amount of energy. As a fun and rough prediction, treat the person as an isolated heat engine, operating between the internal temperature of 37°C (98.6°F) and the ambient air temperature of 20°C.

A particular car does work at the rate of about 7.0 kJ/s when traveling at a steady 21.8 m/s along a level road. This is the work done against friction. The car can travel 17 km on 1.0 L of gasoline at this speed (about 40 mi/gal). What is the minimum value for T_H if T_L is 25°C? The energy available from 1.0 L of gas is 3.2 x 10⁷ J.

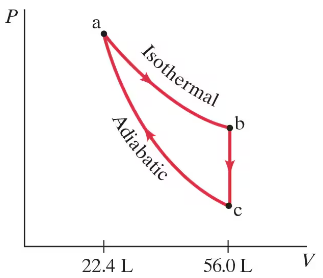
The working substance of a certain Carnot engine is 1.0 mol of an ideal monatomic gas. During the isothermal expansion portion of this engine’s cycle, the volume of the gas doubles, while during the adiabatic expansion the volume increases by a factor of 6.2. The work output of the engine is 920 J in each cycle. Compute the temperatures of the two reservoirs between which this engine operates.

One mole of monatomic gas undergoes a Carnot cycle with T_H = 350°C and T_L = 210°C. The initial pressure is 8.8 atm. During the isothermal expansion, the volume doubles. Find the values of the pressure and volume at the points a, b, c, and d of Fig. 20–5.

One mole of monatomic gas undergoes a Carnot cycle with T_H = 350°C and T_L = 210°C. The initial pressure is 8.8 atm. During the isothermal expansion, the volume doubles. Calculate the efficiency of the cycle using Eqs. 20–1 and 20–3.

(II) 1.00 mole of nitrogen (N₂) gas and 1.00 mole of argon (Ar) gas are in separate, equal-sized, insulated containers at the same temperature. The containers are then connected and the gases (assumed ideal) allowed to mix. What is the change in entropy

(a) of the system

(II) What is the temperature inside an ideal refrigerator–freezer that operates with a COP = 7.0 in a 22°C room?

What is the coefficient of performance of an ideal heat pump that extracts heat from 6°C air outside and deposits heat inside a house at 24°C?

An ideal heat pump is used to maintain the inside temperature of a house at Tᵢₙ = 22°C when the outside temperature is Tₒᵤₜ. Assume the heat pump does work at a rate of 1700 W. Also assume that the house loses heat via conduction through its walls and other surfaces at a rate given by ( 650 W/C°) (Tᵢₙ - Tₒᵤₜ). If the outside temperature is less than you just calculated, what happens?

How much less per year would it cost a family to operate a heat pump that has a coefficient of performance of 2.9 than an electric heater that costs $2100 to heat their home for a year? If the conversion to the heat pump costs $15,000, how long would it take the family to break even on heating costs? How much would the family save in 20 years?

If 0.45 kg of water at 100°C is changed by a reversible process to steam at 100°C, determine the change in entropy of the surroundings.

If 0.45 kg of water at 100°C is changed by a reversible process to steam at 100°C, determine the change in entropy of the universe as a whole.

If 0.45 kg of water at 100°C is changed by a reversible process to steam at 100°C, determine the change in entropy of the water, the surroundings, and the universe as a whole. How would your answers differ if the process were irreversible?

Why would you expect the total entropy change in a Carnot cycle to be zero?

Why would you expect the total entropy change in a Carnot cycle to be zero? Do a calculation to show that it is zero.

A general theorem states that the amount of energy that becomes unavailable to do useful work in any process is equal to T_L∆S, where T_L is the lowest temperature available and ∆S is the total change in entropy during the process. Show that this is valid in the specific cases of a falling rock that comes to rest when it hits the ground.

Use Eq. 20–14 to determine the entropy of each of the five macrostates listed in Table 20–1 on page 595.

Suppose that you repeatedly shake six coins in your hand and drop them on the floor. Construct a table showing the number of microstates that correspond to each macrostate. What is the probability of obtaining three heads and three tails?

Suppose that you repeatedly shake six coins in your hand and drop them on the floor. Construct a table showing the number of microstates that correspond to each macrostate. What is the probability of obtaining six heads?

(II) Calculate the probabilities, when you throw two dice, of obtaining a 7.

(II) Calculate the probabilities, when you throw two dice, of obtaining an 11.

At a steam power plant, steam engines work in pairs, the heat output of the first one being the approximate heat input of the second. The operating temperatures of the first are 750°C and 440°C, and of the second 415°C and 240°C. If the heat of combustion of coal is 2.8 x 10⁷ J/kg, at what rate must coal be burned if the plant is to put out 950 MW of power? Assume the efficiency of the engines is 65% of the ideal (Carnot) efficiency.

1.00 mole of an ideal monatomic gas at STP first undergoes an isothermal expansion so that the volume at b is 2.5 times the volume at a (Fig. 20–25). Next, heat is extracted at a constant volume so that the pressure drops. The gas is then compressed adiabatically back to the original state. Calculate the pressures at b and c.

Two 1100-kg cars are traveling 75 km/h in opposite directions when they collide and are brought to rest. Estimate the change in entropy of the universe as a result of this collision. Assume T = 20°C.

Suppose a heat pump has a stationary bicycle attachment that allows you to provide the work instead of using an electrical wall outlet. If your heat pump has a coefficient of performance of 2.0 and you can cycle at a racing pace output of about 200 W for a half hour, how much heat can you provide?

A dehumidifier removes water vapor from air and has been referred to as a “refrigerator with an open door.” The humid air is pulled in by a fan and passes over a cold coil, whose temperature is less than the dew point, and some of the air’s water condenses. After this water is extracted, the air is warmed back to its original temperature and sent into the room. In a well-designed dehumidifier, the heat that is removed by the cooling coil mostly comes from the condensation of water vapor to liquid, and this heat is used to re-warm the air. Estimate how much water is removed in 1.0 h by an ideal dehumidifier, if the temperature of the room is 25°C, the water condenses at 8°C, and the dehumidifier does work at the rate of 550 W of electrical power.

A bowl contains many red, orange, and green jelly beans, in equal numbers. You are to make a line of 3 jelly beans by randomly taking 3 beans from the bowl. Construct a table showing the number of microstates that correspond to each macrostate.

A bowl contains many red, orange, and green jelly beans, in equal numbers. You are to make a line of 3 jelly beans by randomly taking 3 beans from the bowl. Construct a table showing the number of microstates that correspond to each macrostate. Then, determine the probability of all 3 beans red.