Determine the phase constant ϕ in Eq. 14–4 if, at t = 0, the oscillating mass is at 𝓍 = ― 1/2 A.

Determine the phase constant ϕ in Eq. 14–4 if, at t = 0, the oscillating mass is at 𝓍 = ― A.

Determine the phase constant ϕ in Eq. 14–4 if, at t = 0, the oscillating mass is at 𝓍 = A .

A 0.25-kg mass at the end of a spring oscillates 3.2 times per second with an amplitude of 0.15 m. Determine the equation describing the motion of the mass, assuming that at t = 0, 𝓍 was a maximum.

An object with mass 2.7 kg is executing simple harmonic motion, attached to a spring with spring constant k = 310 N/m. When the object is 0.020 m from its equilibrium position, it is moving with a speed of 0.60 m/s. Calculate the maximum speed attained by the object.

A mass resting on a horizontal, frictionless surface is attached to one end of a spring; the other end of the spring is fixed to a wall. It takes 3.2 J of work to compress the spring by 0.13 m. The mass is then released from rest and experiences a maximum acceleration of 12m/s². Find the value of the spring constant.

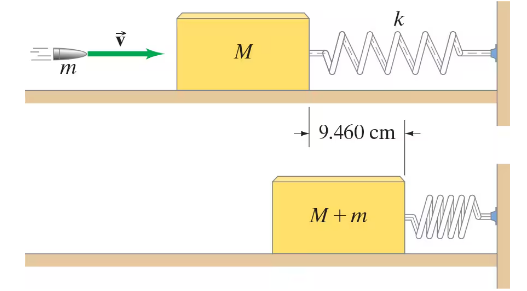
Agent Arlene devised the following method of measuring the muzzle velocity of a rifle (Fig. 14–34). She fires a bullet into a 4.148-kg wooden block resting on a smooth surface, and attached to a spring of spring constant k = 162.7 N/m. The bullet, whose mass is 7.450 g, remains embedded in the wooden block. She measures the maximum distance that the block compresses the spring to be 9.460 cm. What is the speed υ of the bullet?

At t = 0, an 885-g mass at rest on the end of a horizontal spring (k = 184 N/m) is struck by a hammer which gives it an initial speed of 2.12 m/s. Determine the period and frequency of the motion.

What is the period of a simple pendulum 47 cm long when it is in a freely falling elevator?

A clock pendulum oscillates at a frequency of 2.5 Hz. At t = 0, it is released from rest starting at an angle of 12° to the vertical. Ignoring friction, what will be the position (angle in radians) of the pendulum at t = 0.25 s?

An 1150-kg automobile has springs with k = 14,000 N/m. One of the tires is not properly balanced; it has a little extra mass on one side compared to the other, causing the car to shake at certain speeds. If the tire radius is 42 cm, at what speed will the wheel shake most?

An energy-absorbing car bumper has a spring constant of 410 kN/m. Find the maximum compression of the bumper if the car, with mass 1300 kg, collides with a wall at a speed of 2.0 m/s (approximately 5 mi/h).

A 280-kg wooden raft floats on a lake. When a 68-kg man stands on the raft, it sinks 3.5 cm deeper into the water. When he steps off, the raft oscillates for a while. What is the total energy of oscillation (ignoring damping)?

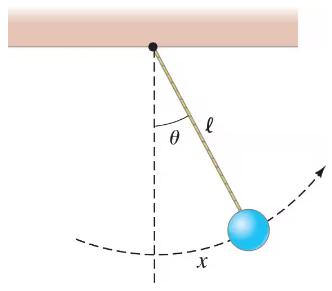
In Section 14–5, the oscillation of a simple pendulum (Fig. 14–48) is viewed as linear motion along the arc length 𝓍 and analyzed via F = ma. Alternatively, the pendulum’s movement can be regarded as rotational motion about its point of support and analyzed using T = Iα. Carry out this alternative analysis and show that θ (t) = θₘₐₓ cos ($\sqrt{\frac{g}{l}}$t + θ), where θ (t) is the angular displacement of the pendulum from the vertical at time t, as long as its maximum value is less than about .