The Earth is not a uniform sphere, but has regions of varying density. Consider a simple model of the Earth divided into three regions—inner core, outer core, and mantle. Let us assume each region has a constant density (the average density of that region in the real Earth). Use this model to predict the average density of the entire Earth.

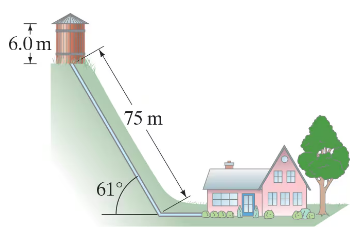
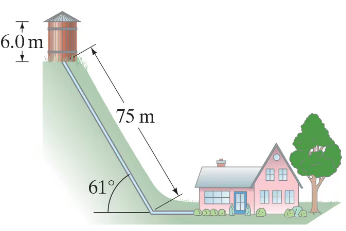
A house at the bottom of a hill is fed by a full tank of water 6.0 m deep and connected to the house by a pipe that is 75 m long at an angle of 61° from the horizontal (Fig. 13–53). Determine the water gauge pressure at the house.

A house at the bottom of a hill is fed by a full tank of water 6.0 m deep and connected to the house by a pipe that is 75 m long at an angle of 61° from the horizontal (Fig. 13–53). How high could the water shoot if it came vertically out of a broken pipe in front of the house?

Determine the minimum gauge pressure needed in the water pipe leading into a building if water is to come out of a faucet on the fourteenth floor, 44 m above that pipe.

An open-tube mercury manometer is used to measure the pressure in an oxygen tank. When the atmospheric pressure is 1040 mbar, what is the absolute pressure (in Pa) in the tank if the height of the mercury in the open tube is 7.6 cm lower than the mercury in the tube connected to the tank? See Fig. 13–10a.

Calculate the true mass (in vacuum) of an aluminum sphere whose apparent mass is 4.0000 kg when weighed in air.

A 0.48-kg piece of wood floats in water but is found to sink in alcohol (SG = 0.79), in which it has an apparent mass of 0.047 kg. What is the SG of the wood?

How many helium-filled balloons would it take to lift a person? Assume the person has a mass of 72 kg and that each helium-filled balloon is spherical with a diameter of 36 cm.

A 12-cm-radius air duct is used to replenish the air of a room 8.2 m x 4.5 m x 3.5 m every 12 min. How fast does the air flow in the duct?

How fast does water flow from a hole at the bottom of a very wide, 5.1-m-deep storage tank filled with water? Ignore viscosity.

What is the volume rate of flow of water from a 1.85-cm-diameter faucet if the pressure head is 12.0 m?

A fish tank has dimensions 36 cm wide by 1.0 m long by 0.60 m high. If the filter should process all the water in the tank once every 2.5 h, what should the flow speed be in the 3.0-cm-diameter input tube for the filter?

Estimate the air pressure inside a category 5 hurricane, where the wind speed is 300 km/h (Fig. 13–56).

<IMAGE>

A fire hose exerts a force on the person holding it due to the water accelerating as it goes from the thicker hose out through the narrow nozzle. How much force is required to hold a 7.0-cm-diameter hose delivering 480 L/min through a 0.75-cm-diameter nozzle?

What must be the pressure difference between the two ends of a 1.6-km section of pipe, 29 cm in diameter, if it is to transport oil (ρ = 950 kg/m³, η=0.20 Pa⋅s) at a rate of 650 cm³/s?

If cholesterol buildup reduces the diameter of an artery by 25%, by what % will the blood flow rate be reduced, assuming the same pressure difference?

Estimate the diameter of a steel needle that can just barely remain on top of water due to surface tension. (See Figs. 13–38 and 13–39a, and Table 13–1.)

A common effect of surface tension is the ability of a liquid to rise up a narrow tube due to capillary action. Show that for a narrow tube of radius r placed in a liquid of density ρ and surface tension γ, the liquid in the tube will reach a height h = 2γ/ρgr above the level of the liquid outside the tube, where g is the gravitational acceleration. Assume that the liquid “wets” the tube and that the liquid surface is vertical at the contact with the inside of the tube.

A 3.2-N force is applied to the plunger of a hypodermic needle. If the diameter of the plunger is 1.3 cm and that of the needle is 0.20 mm, with what force does the fluid leave the needle?

A 3.2-N force is applied to the plunger of a hypodermic needle. If the diameter of the plunger is 1.3 cm and that of the needle is 0.20 mm, what force on the plunger would be needed to push fluid into a vein where the gauge pressure is 75 mm-Hg? Answer for the instant just before the fluid starts to move.

A pump supplies water to a 1.59-cm inner diameter hose that tapers down to a 0.953-cm-diameter nozzle. The nozzle is aimed so water comes out at a 45° angle and lands 3.0 m away. The nozzle is 0.60 m above ground level, and the pump output is essentially at ground level. What pressure is supplied by the pump?

A hydraulic lift is used to jack a 960-kg car 52 cm off the floor. The diameter of the output piston is 18 cm, and the input force is 380 N. What is the area of the input piston?

When you ascend or descend a great deal when driving in a car, your ears “pop,” which means that the pressure behind the eardrum is being equalized to that outside. If this did not happen, what would be the approximate force on an eardrum of area 0.20cm² if a change in altitude of 1120 m takes place?

When a person drives or hikes to a higher altitude, and even more during descent, volume changes of trapped air in the middle ear can cause ear discomfort until the middle-ear pressure and exterior pressure are equalized. If a rapid descent at a rate of 7.0 m/s or faster commonly causes ear discomfort, what is the maximum rate of increase in atmospheric pressure (that is, dP/dt) tolerable to most people?

A ship, carrying fresh water to a desert island in the Caribbean, has a horizontal cross-sectional area of 2240 m² at the waterline. When unloaded, the ship rises 8.55 m higher in the sea. How much water (m³) was delivered?

You are watering your lawn with a hose when you put your finger over the hose opening to increase the distance the water reaches. If you are holding the hose horizontally, and the distance the water reaches increases by a factor of 4, what fraction of the hose opening did you block?

Estimate the total mass of the Earth’s atmosphere, using the known value of atmospheric pressure at sea level.

A drinking fountain shoots water about 12 cm up in the air from a nozzle of diameter 0.60 cm (Fig. 13–67). The pump at the base of the unit (1.1 m below the nozzle) pushes water into a 1.2-cm-diameter supply pipe that goes up to the nozzle. What gauge pressure does the pump have to provide? Ignore the viscosity; your answer will therefore be an underestimate.

<IMAGE>